Salut,
Quand on a de la bouteille, on s'emmerde pas et "on pose" directement
\!=\!g(\theta))
qui est bien définie vu que, bien que
ne soit pas bien défini,
)
l'est quand même du fait de la
-périodicité de
.
Si tu veut le faire "plus conventionnellement", tu peut effectivement poser
\!=\!g(\text{Arg}(z)))
.
- Si
)
est la détermination dans
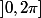
, ça te donne la continuité de
sauf éventuellement en
.
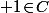
- Si
est la détermination dans
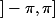
, ça te donne la continuité de
sauf éventuellement en
.
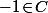
Donc il suffit d'expliquer que, vu la périodicité de
le résultat du calcul de
))
ne dépend pas de la détermination choisie pour
pour démontrer la continuité de
sur
tout entier.
Bref, c'est totalement évident modulo de bien se souvenir qu'il n'y a pas UNE fonction argument, mais DES fonctions argument. Une autre façon de voir le bidule, c'est de comprendre que, certes, il n'y a pas de détermination continue de l'argument sur
tout entier, mais que quelque soit le point
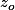
de
, il existe une détermination de l'argument qui est continue au voisinage de
.
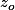
(et si ça t’intéresse, la "théorie" qu'il y a derrière, ça s’appelle celle des "revêtements" : R->C;theta->exp(i.theta) c'est un "revêtement" du cercle trigo. : localement, ça admet des inverses continus)
