Fonction réccurentes

par **juliana1** » 12 Mai 2013, 20:43

bonjour j'ai un problème de résoudre cette fonction dans le cas ou n est une puissance de 2
t(1)=0
t(n)=2t(n/2)+5n

et aussi
t(1)=0
t(n)=t(n/2)+5n-3

enfin un 3eme

on a C1 ,C2 >0 tel que n>P
montrez que
C1*f(n) <= g(n)=n^3 -2n^2 -5n <= C2*f(n)

en déduire la compléxité asymptotique de g(n)

merci beaucoup

par **XENSECP** » 12 Mai 2013, 22:13

Salut,

J'ai un peu cherché et j'ai trouvé ta première. Par contre je sais pas si tu cherches une solution "théorique" ou si une "empirique" te convient (sachant qu'il faut le prouver par récurrence évidemment).

Tiens moi au courant.

par **juliana1** » 12 Mai 2013, 22:21

XENSECP a écrit:Salut,

J'ai un peu cherché et j'ai trouvé ta première. Par contre je sais pas si tu cherches une solution "théorique" ou si une "empirique" te convient (sachant qu'il faut le prouver par récurrence évidemment).

Tiens moi au courant.

ui la solution mathématique s'il vous plait comment la résoudre mathématiquement

par **XENSECP** » 12 Mai 2013, 22:23

Aah les maths... Moi j'ai une solution basée sur de l'empirique pour aboutir à une hypothèse de récurrence. Si ça te va, je peux te la présenter ...

par **juliana1** » 12 Mai 2013, 22:25

XENSECP a écrit:Aah les maths... Moi j'ai une solution basée sur de l'empirique pour aboutir à une hypothèse de récurrence. Si ça te va, je peux te la présenter ...

oui pas de problème

par **XENSECP** » 12 Mai 2013, 22:31

Bon c'est pas une intuition naturelle. J'ai essayé de voir comment ça pouvait "récurrer" avant d'arriver à ça :

J'ai constaté qu'il y avait toujours un facteur 5... Puis que ça dépendait de n et enfin de k en posant

.

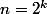
Je suis arrivé du coup à :

par **juliana1** » 12 Mai 2013, 22:37

XENSECP a écrit:Bon c'est pas une intuition naturelle. J'ai essayé de voir comment ça pouvait "récurrer" avant d'arriver à ça :

J'ai constaté qu'il y avait toujours un facteur 5... Puis que ça dépendait de n et enfin de k en posant .

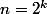
Je suis arrivé du coup à :

mais le problème c'est comment tu as fait pour avoir la dernière equation? tu peux m'expliquez comment stp

par **XENSECP** » 12 Mai 2013, 22:44

Pour la deuxième c'est plus mathématique :

Soit

par **juliana1** » 12 Mai 2013, 22:49

XENSECP a écrit:Pour la deuxième c'est plus mathématique :

Soit

pourquoi le log_2{n}?
en faite j'ai rien compris de l derniere ligne celle de

par **juliana1** » 13 Mai 2013, 07:18

sayez sa marche merci :D
et pour la 3eme Question est ce ue vous connnaissez une réponse?

par **XENSECP** » 13 Mai 2013, 07:57

Il semble manquer des données non ?

par **spike0789** » 13 Mai 2013, 09:10

Bonjour,

Une solution théorique pour la première question :

Si on pose n=2^p, on a :
t(2^p)=2*t(2^(p-1))+5*2^p

On divise le tout par 2^p et on pose U(p)=t(2^p)/2^p

On obtient directement que U est arithmétique de raison 5
Donc U(p)=5p et on obtient exactement le même résultat que XENSECP.

par **juliana1** » 13 Mai 2013, 14:46

XENSECP a écrit:Il semble manquer des données non ?

c'est le suivi de la question

t(1)=0
t(n)=t(n/2)+5n-3

par **juliana1** » 13 Mai 2013, 14:47

spike0789 a écrit:Bonjour,

Une solution théorique pour la première question :

Si on pose n=2^p, on a :
t(2^p)=2*t(2^(p-1))+5*2^p

On divise le tout par 2^p et on pose U(p)=t(2^p)/2^p

On obtient directement que U est arithmétique de raison 5
Donc U(p)=5p et on obtient exactement le même résultat que XENSECP.

ce n'est pas les suites reccurentes mais les equaions recurrentes

par **spike0789** » 13 Mai 2013, 14:54

juliana1 a écrit:et aussi
t(1)=0
t(n)=t(n/2)+5n-3

enfin un 3eme

on a C1 ,C2 >0 tel que n>P
montrez que
C1*f(n) <= g(n)=n^3 -2n^2 -5n <= C2*f(n)

en déduire la compléxité asymptotique de g(n)

merci beaucoup

Que vaut f(n) ? p?

juliana1 a écrit:ce n'est pas les suites reccurentes mais les equaions recurrentes

?? Je ne comprends pas ta remarque...

Fonction réccurentes

fonction réccurentes

Qui est en ligne