Fonction non développable en série entière

[Engel10]

Bonjour à tous.
Je lisais mon cours et comme ça il est dit que la fonction f :⃗R → ⃗R qui à tout x associe 0 si x ≤ 0 et exp(-1/x²) si x>0 est de classe C infini sur ⃗R, mais elle n′admet pas de developpement en serie entière.
C′est ce que je n′arrive pas à comprendre.


la fonction qui à tout x associe -1/x est de classe C infini sur ⃗R*+ .
la fonction qui à tout x associe exp(x) est aussi de classe C infini. Donc exp(-1/x²) est de classe C infini si x > 0.
Si x≤0 la derivée n-ieme de f est nulle donc f est de classe C infini si x ≤ 0.
On deduit ainsi que f est de classe C infini sur ⃗R.

maintenant, le fait que f ne soit pas developpable en serie entiere, c′est ce qui me pose probleme. Un theorème dans mon cours dit que si f est de classe C infini, il faut que la limite quand n → +∞ du reste integrale du polynôme de Taylor tende vers 0. Mais ça je trouve ça un peu difficile à calculer.

Merci d′avance pour vos reponses.

[GaBuZoMeu]

Si f était développable en série entière au voisinage de l'origine, son développement en série entière serait donné par sa série de Taylor en 0. Or tu as calculé les dérivées successives en 0, elles sont toutes nulles et la série de Taylor est donc la série nulle. Mais la somme de la série nulle, c'est la fonction constante nulle !!!

[tournesol]

Le reste intégral est alors facile à calculer puisqu'il est égal à la fonction indépendamment de l'ordre.
il ne peut donc pas tendre uniformement vers zéro .

[Engel10]

Si f était développable en série entière au voisinage de l'origine, son développement en série entière serait donné par sa série de Taylor en 0. Or tu as calculé les dérivées successives en 0, elles sont toutes nulles et la série de Taylor est donc la série nulle. Mais la somme de la série nulle, c'est la fonction constante nulle !!!

Merci pour ta réponse.
OK si je comprend bien, en réalité, c'est parce que f ne peut pas s'écrire de la forme ∑ aₙxⁿ avec aₙxⁿ ≠ 0 pour tout x pris dans un intervalle centré et ouvert de ⃗R, qu′on dit qu′elle n′est pas développable en serie entière. n′est ce pas ?

Merci d′avance.

[pascal16]

on peut sans doute écrire f le DL de f partout sauf en 0

fo que je regarde si on développe en 1 si la fonction et son développement divergent l'un de l'autre pour x<0

[tournesol]

Cette fonction est analytique sur

[Engel10]

Merci pour ta réponse.
OK si je comprend bien, en réalité, c'est parce que f ne peut pas s'écrire de la forme ∑ aₙxⁿ avec aₙxⁿ ≠ 0 pour tout x pris dans un intervalle centré et ouvert de ⃗R, qu′on dit qu′elle n′est pas développable en serie entière. n′est ce pas ?

Svp je veux savoir si mon raisonnement est correcte.

[Engel10]

......

[Tuvasbien]

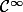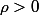Non ton raisonnement n'est pas bon, une fonction est développable en série entière au voisinage de s'il existe telle que pour tout dans un voisinage de . Si tel est le cas, alors est de classe à l'intérieur du disque de convergence autour de de sorte que . Si ta fonction était développable en série entière au voisinage de , il existerait tel que avec . Tu peux montrer par récurrence que pour tout il existe un polynôme tel que , le théorème de prolongement de la dérivée permet alors d'affirmer que toutes les dérivées de en sont nulles et par suite que tous les coefficients sont nuls et donc que est nulle au voisinage de ce qui n'est pas donc n'est pas développable en série entière au voisinage de .

[Engel10]

Merci beaucoup, je vois