Fonction identité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yoshiop
- Membre Naturel
- Messages: 11
- Enregistré le: 08 Oct 2019, 20:14
-
 par yoshiop » 01 Nov 2019, 17:14
par yoshiop » 01 Nov 2019, 17:14
Bonjour,
je bloque sur cette exercice :
1) Soit

,

:

dans

definie par
=|x|)
et
=x^2+1)
ici comment peut ont faire pour chercher les images de f et g ? j'ai pensé à faire
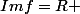
par double inclusion et pareil pour g mais peut être que je cherche beaucoup trop compliqué

.
merci.
Modifié en dernier par
yoshiop le 04 Nov 2019, 20:37, modifié 2 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6141
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Nov 2019, 18:12
par GaBuZoMeu » 01 Nov 2019, 18:12
Pour 1) : un petit dessin pourrait t'aider !
Pour 2) :

veut simplement dire que pour tout élément
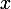
de
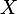
,
)=x)
.
Avec ça, il n'est pas trop dur de démontrer que tout élément de
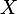
a un antécédent par
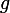
et que si deux éléments de
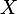
ont la même image par

, alors ils sont égaux.
-
yoshiop
- Membre Naturel
- Messages: 11
- Enregistré le: 08 Oct 2019, 20:14
-
 par yoshiop » 01 Nov 2019, 20:19
par yoshiop » 01 Nov 2019, 20:19
rebonjour,
désolé mais je ne comprend toujours pas. J'ai déjà fais un graph pour f et g mais mathématiquement je n'arrive pas.
pour la 2) il faut donc démontrer que
=x)
?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6141
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Nov 2019, 20:43
par GaBuZoMeu » 01 Nov 2019, 20:43
Mais non ! Le fait que
)=x)
pour tout
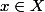
, c'est l'hypothèse !
Tu ne vois pas que
=x)
pour tout
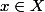
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités