bonjour à tous
je dois resoudre l'equation suivante
(exp(x))² -4e(x) -1=0
j'ai remplacé e(x) par X
cela me donne à resoudre
X²-4X-1=0
Je trouve 4.236 et -0.236
comment je fait ensuite pour revenir sur mon équation et trouver les résultats?
merci pour votre aide
Fonction exponentielle à resoudre
4 messages
- Page 1 sur 1
Re: fonction exponentielle à resoudre
Salut,
Quand tu trouves X=4.236 ou X=-0.236, ça veut dire que exp(x)=4.236 ou exp(x)=-0,236
Il faut donc résoudre ces deux équations pour trouver x. Sachant que la deuxième n'a pas de solution (pourquoi ?)
Remarque: il faut vraiment garder les valeurs exactes dans ta résolution.
Quand tu trouves X=4.236 ou X=-0.236, ça veut dire que exp(x)=4.236 ou exp(x)=-0,236
Il faut donc résoudre ces deux équations pour trouver x. Sachant que la deuxième n'a pas de solution (pourquoi ?)
Remarque: il faut vraiment garder les valeurs exactes dans ta résolution.
Pseudo modifié : anciennement Trident2.
Re: fonction exponentielle à resoudre
regarde la question suivante dans le sujet de bac, tu as la valeur exacte de donnée.
c'est une astuce à retenir
c'est une astuce à retenir
Re: fonction exponentielle à resoudre
Bonjour,
C'est une erreur classique que je rencontre fréquemment : en maths, ne JAMAIS JAMAIS JAMAIS remplacer les valeurs exactes par des valeurs approchées (sauf si l'énoncé le demande, mais c'est une parenthèse).
Ainsi, la valeur exacte de , c'est
, c'est  et sûrement pas 3,14 ni 3,1416 ni 3,141592...
et sûrement pas 3,14 ni 3,1416 ni 3,141592...
Les valeurs approchées permettent de "voir" où on se situe (ordre de grandeur, vraisemblance du résultat...) mais posent plusieurs problèmes :
Evidemment, c'est vrai en math, mais pas dans la vraie vie : si j'ai un terrain circulaire, je ne vais pas acheter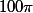 mètres de clôture, mais 315 mètres de clôture !
mètres de clôture, mais 315 mètres de clôture !
C'est une erreur classique que je rencontre fréquemment : en maths, ne JAMAIS JAMAIS JAMAIS remplacer les valeurs exactes par des valeurs approchées (sauf si l'énoncé le demande, mais c'est une parenthèse).
Ainsi, la valeur exacte de
Les valeurs approchées permettent de "voir" où on se situe (ordre de grandeur, vraisemblance du résultat...) mais posent plusieurs problèmes :
- cela complexifie les calculs : ainsi
ne se calcule pas alors que
nécessite un calcul (qui peut être douloureux...)
- les valeurs approchées ont un écart avec les valeurs exactes, et cet écart s'amplifie au fur et à mesure des calculs.
- Ainsi, avec les calculatrices usuelles du bac, la suite définie par
puis
montrent une divergence vers
pour l'une des calculatrices, vers
pour l'autre,
- alors qu'en conservant les valeurs exactes cette suite est constante (cela vient de l'erreur d'arrondi qui "tronque" les décimales, et la variation de l'erreur est exponentielle avec
)
- Ainsi, avec les calculatrices usuelles du bac, la suite définie par
Evidemment, c'est vrai en math, mais pas dans la vraie vie : si j'ai un terrain circulaire, je ne vais pas acheter
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
