Fonction définie

[quentin0105]

Bonjour,

Voilà j'aimerais savoir si mon exercice est correcte :

énoncer :

Soit f une fonction définie sur R par f(x)= 10-x^3+2,5x²+2x
1) Donner les limites de f en -infini et +infini.
2) Déterminer le nombre dérivé f'(x) pour tout réel x.
3) étudier les variations f sur R

Voici ce que j'ai fais :

1) lim x-> -infini f(x)=+infini
lim x-> +infini f(x)=-infini

2) f(x)= 10-x^3+2,5x²+2x
= -3x²+2,5*2x+2
= -3x²+5x+2

3)
x -infini -5 -2 +infini

10-3x^3 + + +

2,5x² + O - -

2x + + O -

10-x^3+2.5x²+2x + - +

10-x^3=0

2,5x²=0
2,5*2x
x=-5

2x=0
x=-2

Je ne comprends pas trop le 3 pourriez vous m'aidez?

Cordialement,
Quentin

[mrif]

Bonjour,

Voilà j'aimerais savoir si mon exercice est correcte :

énoncer :

Soit f une fonction définie sur R par f(x)= 10-x^3+2,5x²+2x
1) Donner les limites de f en -infini et +infini.
2) Déterminer le nombre dérivé f'(x) pour tout réel x.
3) étudier les variations f sur R

Voici ce que j'ai fais :

1) lim x-> -infini f(x)=+infini
lim x-> +infini f(x)=-infini

2) f(x)= 10-x^3+2,5x²+2x
= -3x²+2,5*2x+2
= -3x²+5x+2

3)
x -infini -5 -2 +infini

10-3x^3 + + +

2,5x² + O - -

2x + + O -

10-x^3+2.5x²+2x + - +

10-x^3=0

2,5x²=0
2,5*2x
x=-5

2x=0
x=-2

Je ne comprends pas trop le 3 pourriez vous m'aidez?

Cordialement,
Quentin

1) et 2) c'est bon mais pour le 3) c'est pas du tout ça.
Tu dois étudier le signe de la dérivée f'(x) = -3x²+5x+2
Pour cela tu résouds l'équation : -3x²+5x+2 = 0
Je te laisse faire déjà ça et continuer et si tu bloques, tu reviens.

[Archibald]

Bonsoir

C'est un exercice-type Bac où on te demande de calculer :
1) les limites d'une fonction f (puis éventuellement d'en déduire les asymptotes)
2) la dérivée d'une fonction et son tableau de signe
3) d'en déduire le tableau de variation de la fonction f

Tu sais que f est croissante si et décroissante si , d'où l'importance de l'étude du signe de f'

Ta fonction dérivée est un trinôme du second degré (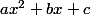 ), tu dois donc calculer son discriminant d'abord ( )

[quentin0105]

>voilà j'ai commencer à faire ceci :

f(x)=-3x²+5x+2=0
ax²+bx+c

/\=b²-4a.c
=5²-4*(-3)*2
=25+24
=49>0

Donc deux racines :

= -(5)-racine carrée 49/2*(-3)
= -12/-6
= 2


= -(5)+racine carrée 49/2*(-3)
= 2/-6
= -0.33

[mrif]

>voilà j'ai commencer à faire ceci :

f(x)=-3x²+5x+2=0
ax²+bx+c

/\=b²-4a.c
=5²-4*(-3)*2
=25+24
=49>0

Donc deux racines :

= -(5)-racine carrée 49/2*(-3)
= -12/-6
= 2


= -(5)+racine carrée 49/2*(-3)
= 2/-6
= -0.33

En mathématiques, on ne donne une valeur approchée que quand c'est demandé. Ta dérivée s'annule en 2 et -1/3. Comme le coefficient de x² est négatif, la dérivée est positive à l'interieur des racines et négativé à l'extérieur. Cela te permettra de construire ton tableau de variation.

[quentin0105]

En mathématiques, on ne donne une valeur approchée que quand c'est demandé. Ta dérivée s'annule en 2 et -1/3. Comme le coefficient de x² est négatif, la dérivée est positive à l'interieur des racines et négativé à l'extérieur. Cela te permettra de construire ton tableau de variation.

D'accord merci bien
Voici le tableau :

x -infini -1/3 2 +infini

f'(x) - + -

f(x) Négatif Positif Négatif
-infini 9,64 16 +infini

[Archibald]

D'accord merci bien
Voici le tableau :

x -infini -1/3 2 +infini

f'(x) - + -

f(x) Négatif Positif Négatif
-infini 9,64 16 +infini

On ne te demande pas le signe de f mais son sens de variation (d'où le calcul de sa dérivée). Si la dérivée f' est positive sur un intervalle, f croît sur cet intervalle. Et vice-versa..

[quentin0105]

On ne te demande pas le signe de f mais son sens de variation (d'où le calcul de sa dérivée). Si la dérivée f' est positive sur un intervalle, f croît sur cet intervalle. Et vice-versa..

Je ne comprend pas.

Il nous demande juste la direction des flèches?

[Archibald]

Je ne comprend pas.

Il nous demande juste la direction des flèches?

Oui... elles indiquent le sens de variation de ta fonction.

[quentin0105]

D'accord merci bien de m'avoir aider :)