Bonjour tout le monde,
J'apprécierais si quelqu'un pourrais m'aider avec les questions suivantes:
f(x)=x/x^2+9x+41
a) Find the smallest real number r such that f(x) is decreasing for all x greater than r
b) Find the smallest integer s such that f(n) is decreasing for all
integers n greater than or equal to s.
Désolée pour l'anglais, je me suis dis que c'était mieux de la laissé telle qu'elle que de risquer de mal la traduire.
An=6n/4n+15
a) Quel est la limite de cette séquence
b) Quelle est la somme de cette série ?
Un énorme merci a tous ceux qui m'aideront à y voir plus clair !
Fonction décroissante +séries et séquences
8 messages
- Page 1 sur 1
Bonsoir
Jouons à la devinette.
chlochlo3d, tu veux parler de=\dfrac{x}{x^2+9x+41},) je suppose.
je suppose.
On peut traduire les deux questions a) et b) par:
a) Trouver le plus petit nombre réel r tel que f est décroissante sur [r,+\infty[. En d'autres termes trouver le plus grand intervalle (au sens de l'inclusion) sur lequel f est décroissante.
sur lequel f est décroissante.
b) Trouver le plus petit nombre entier s à partir duquel la suite f(n) est décroissante.
Pour ça, étudies la fonction f.
Jouons encore à le devinette.
chan79 a écrit:Salut
Mets les parenthèses pour qu'il n'y ait pas d'ambiguïté
Jouons à la devinette.
chlochlo3d, tu veux parler de
On peut traduire les deux questions a) et b) par:
a) Trouver le plus petit nombre réel r tel que f est décroissante sur [r,+\infty[. En d'autres termes trouver le plus grand intervalle (au sens de l'inclusion)
b) Trouver le plus petit nombre entier s à partir duquel la suite f(n) est décroissante.
Pour ça, étudies la fonction f.
Jouons encore à le devinette.
Désolée pour les parenthese, oui je parles vraiment des fonctions que Deltab a mis (comment les fait-on d'ailleurs ?)
Pour trouver où une fonction est décroissante, je sais qu'il faut que sont dérivé soit négatif , alors le dérivé serait
(x^2+9x+41)- x(2x+9)
___________________
(x^2+9x+41)^2
Mais la encore, ca ne m'avance pas.
Pour trouver où une fonction est décroissante, je sais qu'il faut que sont dérivé soit négatif , alors le dérivé serait
(x^2+9x+41)- x(2x+9)
___________________
(x^2+9x+41)^2
Mais la encore, ca ne m'avance pas.
Salut,
Si=\frac{x}{x^2+9x+41}\) alors effectivement,
alors effectivement, =\frac{1\times(x^2+9x+41)-x\times (2x+9)}{x^2+9x+41}\) et, vu que ce sont tout les deux des polynômes du second degré, on trouve sans difficulté le signe du numérateur et du dénominateur de
et, vu que ce sont tout les deux des polynômes du second degré, on trouve sans difficulté le signe du numérateur et du dénominateur de ) ce qui donne le signe de
ce qui donne le signe de  et permet de répondre à la question a).
et permet de répondre à la question a).
Pour la b), il suffit d'étudier le signe de-f(n)=\frac{(n+1)(n^2+9n+41)-n((n+1)^2+9(n+1)+41)}{((n+1)^2+9(n+1)+41)(n^2+9n+41)}\) qui, de nouveau, n'est formé que de polynomes du second degré...
qui, de nouveau, n'est formé que de polynomes du second degré...
Si
Pour la b), il suffit d'étudier le signe de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour.
>>Ben314
Petite erreur dans le calcul de) , le dénominateur doit être au carré et on n'aura pas à étudier son signe.
, le dénominateur doit être au carré et on n'aura pas à étudier son signe.
=\dfrac{1\times(x^2+9x+41)-x\times (2x+9)}{(x^2+9x+41)^2}}) .
.
Pour b) Si on a trouvé le plus grand intervalle sur lequel f est décroissante, on en déduit que la suite
sur lequel f est décroissante, on en déduit que la suite 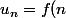) [B]est décroissante si
[B]est décroissante si  , sinon décroissante [/B] à partir au moins du rang
, sinon décroissante [/B] à partir au moins du rang 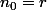 si
si  est entier sinon à partir du rang
est entier sinon à partir du rang  où [r] est la partie entière de
où [r] est la partie entière de  . Il reste à trouver pour
. Il reste à trouver pour 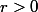 , le plus petit entier s à partir du quel
, le plus petit entier s à partir du quel 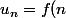) est décroissante,
est décroissante,  .
.
>>Ben314
Petite erreur dans le calcul de
Pour b) Si on a trouvé le plus grand intervalle
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
