Bonjour,
Voici un énoncé et la solution. Je viens vers vous car j'ai du mal à comprendre la démonstration.
Soit f : [0, 1] → [0, 1] une fonction croissante. Montrer que f admet un point fixe.
Solution
{x ∈ [0, 1] /f (x) >= x} est non vide (0 y appartient) et est majoré (par 1).
On peut donc poser α = sup{x ∈ [0,1]/f(x) >=x}.
Pour tout x > α, on a f(x) < x donc f(α) <= f(x) < x.
Puisque f(α) <= x pour tout x > α, on a aussi f(α) <= α. *
Pour tout x < α, il existe t ∈ ]x,α] tel que f(t)>= t donc f(α) >= f(t) >= t >=x. Puisque ceci vaut pour tout x < α, on a aussi f(α)>= α.
Finalement f(α) = α.
* Première assertion que je comprend pas
Je comprend le raisonnement de d'abord montrer inférieur ou égal, puis supérieur ou égal. C'est les arguments qui permettent d'affirmer cela qui me semblent insuffisants (même si je me doute que j'ai tord et que quelque chose m'échappe.)
Merci de votre aide.
Fonction croissante et point fixe
9 messages
- Page 1 sur 1
Re: Fonction croissante et point fixe
Bonsoir,
Effectivement, c'est un peu long à digérer, mais pour te faciliter la compréhension, commence par tracer ton repère ainsi que les intervalles [0,1] pour les x et [0,1] pour les y.
Prends deux valeurs f(0) et f(1) et essais de les relier par une courbe, tu pourras constater qu'à un moment cette courbe coupe la droite y=x (bien entendu elle peut le couper à plusieurs reprises en restant croissante, donc elle aura dans ce cas plusieurs points fixes).
On commence par {x ∈ [0, 1] /f (x) >= x} car on notre se trouve au départ au dessus de la droite y=x car f(0)>0 (sauf pour le cas f(0)=0 dans ce cas 0 est point fixe) et on cerce quand notre courbe passe de l'autre cote de la droite y=x.
J'espère que cela peut t'aider.
Effectivement, c'est un peu long à digérer, mais pour te faciliter la compréhension, commence par tracer ton repère ainsi que les intervalles [0,1] pour les x et [0,1] pour les y.
Prends deux valeurs f(0) et f(1) et essais de les relier par une courbe, tu pourras constater qu'à un moment cette courbe coupe la droite y=x (bien entendu elle peut le couper à plusieurs reprises en restant croissante, donc elle aura dans ce cas plusieurs points fixes).
On commence par {x ∈ [0, 1] /f (x) >= x} car on notre se trouve au départ au dessus de la droite y=x car f(0)>0 (sauf pour le cas f(0)=0 dans ce cas 0 est point fixe) et on cerce quand notre courbe passe de l'autre cote de la droite y=x.
J'espère que cela peut t'aider.
Re: Fonction croissante et point fixe
Bonjour,
En fait, toute cette partie la, je la comprend. C'est d'ailleurs la partie que j'avais réussi sans le corrige. J'avais également fais une "démonstration" graphique. C'est à partir du moment où le corrige utilise le a, avec les implications, que ca se complique. Notamment le passage où j'ai mis un *
Merci
En fait, toute cette partie la, je la comprend. C'est d'ailleurs la partie que j'avais réussi sans le corrige. J'avais également fais une "démonstration" graphique. C'est à partir du moment où le corrige utilise le a, avec les implications, que ca se complique. Notamment le passage où j'ai mis un *
Merci
Re: Fonction croissante et point fixe
On veut montrer \leq a) .
.
Si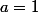 , c'est trivialement vrai.
, c'est trivialement vrai.
Supposons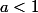 . Alors pour tout
. Alors pour tout 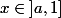 on a
on a  <x) , et donc
, et donc \leq f(x)<x) .
.
Autrement dit (en posant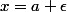 ) pour tout
) pour tout  tel que
tel que 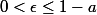 , on a
, on a < a+\epsilon) .
.
Ceci entraîne\leq a) .
.
Si
Supposons
Autrement dit (en posant
Ceci entraîne
Re: Fonction croissante et point fixe
Ok merci robot.
La dernière implication n'est toujours pas hyper logique dans mon esprit puisque e est strictement supérieur à 0. Mais je pense pas qu'on puisse m'expliquer mieux que ce que tu viens de faire. Je vais y réfléchir encore et encore jusqu'à ce que ca vienne
La dernière implication n'est toujours pas hyper logique dans mon esprit puisque e est strictement supérieur à 0. Mais je pense pas qu'on puisse m'expliquer mieux que ce que tu viens de faire. Je vais y réfléchir encore et encore jusqu'à ce que ca vienne
Re: Fonction croissante et point fixe
Si  - a) est plus petit que tout
est plus petit que tout 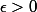 , ça ne te semble pas hyper-logique d'en déduire qu'il est négatif ou nul ?
, ça ne te semble pas hyper-logique d'en déduire qu'il est négatif ou nul ?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
