Fonction de classe Cn

[welcome]

Bonjour , j'ai besoin d'aide svp pour cette question ,
merci

[Ben314]

Salut,
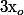
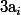
On fixe un . Si est l'un des , le résultat est trivial.
Sinon, on pose et on considère la fonction (pour ) qui est évidement de classe .
Combien de fois (au moins) s'annule t'elle sur ?
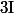
Que peut on en déduire sur le nombre de zéros (distincts) de ? de ? . . . de ?
Que vaut ?
Conclusion.

[welcome]

g s'annule (au moins) n fois sur I , g' n-1 fois , g" n-2 fois ...
est ce vrai ??

[alavacommejetepousse]

c'est la formule des n niveaux tu as oublié une solution

[Ben314]

Tout est juste (le fait que, si une fonction h s'annule p>1 fois sur un intervalle I alors h' s'annule au moins p-1 fois vient simplement du théorème de Rolles)
Sauf que, parti comme ça, tu arrive à s'annule au moins... 0 fois ce qui n'est pas terrible-terrible comme constatation.

Cherche un peu mieux le nombre de zéros de g : pour le moment tu n'utilise absolument pas le fait que la constante k n'est pas du tout tirée au hasard mais prise de façon à ce que...