Fonction borelienne

[Anonyme]

Salut ,
Quelqu un a t il une idée sur cet exercice ?

f est une fonction strictement croissante de R vers R (donc borélienne)
1)l image reciproque d un non borelien peut il etre borelien?
2)Montrer que l image directe d intervalle de la forme [a,oo[ est un borelien
3) Montrer que si B est un borelien alors f(B) est aussi borelien
Merci.
Rosie

[redwolf]

Bonsoir.

Question 1)

Si f est continue, c'est un homéomorphisme, et l'image réciproque d'un non-borélien ne peut être borélienne, sans quoi le non-borélien de départ serait l'image réciproque d'un borélien par une application continue (à savoir la réciproque de f).

Si f n'est pas continue, il existe un intervalle qui n'est pas du tout atteint par f. L'image réciproque d'un non-borélien d'un tel intervalle est l'ensemble vide, c'est à dire un borélien. Si tu veux un contrexemple sans ensemble vide, il suffit de réunir un tel non-borélien et un borélien quelconque d'image réciproque non vide...

[Anonyme]

Bonsoir.

Question 1)

Si f est continue, c'est un homéomorphisme, et l'image réciproque d'un non-borélien ne peut être borélienne, sans quoi le non-borélien de départ serait l'image réciproque d'un borélien par une application continue (à savoir la réciproque de f).

Si f n'est pas continue, il existe un intervalle qui n'est pas du tout atteint par f. L'image réciproque d'un non-borélien d'un tel intervalle est l'ensemble vide, c'est à dire un borélien. Si tu veux un contrexemple sans ensemble vide, il suffit de réunir un tel non-borélien et un borélien quelconque d'image réciproque non vide...

Merci pour la reponse .

[El_Gato]

Si f est strictement croissante l'ensemble de ses points de discontinuité est au plus dénombrable et f coincide pp avec un homéomorphisme.

f coincide donc presque partout avec une fonction bi-mesurable. En conséquence:

1) l'image réciproque d'un non borélien ne peut être borélien.
2) et 3) L'image directe d'un et plus généralement de tout borélien est un borélien.

[redwolf]

Bonjour El_Gato.

Comment ça, elle coïncide presque partout avec un homéomorphisme ? Si c'était le cas, elle coïnciderait en tous ses points de continuité. Imaginons une fonction f strictement croissante qui n'a qu'une discontinuité. Quel est l'homéomorphisme qui coïncide avec elle sauf en un point ?

[El_Gato]

Bonjour El_Gato.

Comment ça, elle coïncide presque partout avec un homéomorphisme ? Si c'était le cas, elle coïnciderait en tous ses points de continuité. Imaginons une fonction f strictement croissante qui n'a qu'une discontinuité. Quel est l'homéomorphisme qui coïncide avec elle sauf en un point ?

L'ensemble des points de discontinuité de f est dénombrable: presque partout en x, f est localement un homéo autour de x. Donc f est bi-mesurable, c'est le point important pour cet exo.

[redwolf]

Bonsoir.

Sans vouloir pinailler, je pense que c'est encore faux.
On peut construire une fonction strictement croissante dont l'ensemble des discontinuités (bien que dénombrable) est dense et dont l'ensemble des points de continuité est également dense.

Par exemple la fonction "dédoublement des chiffres binaires" de [0,1[ dans lui-même (qui à .01011010001... par exemple associe .0011001111001100000011...) répond à ces critères. Ses points de discontinuité sont les nombres dont l'écriture binaire est finie. On peut facilement la prolonger à tout entier si on en a envie.

Eh bien pour une telle fonction , on ne peut pas dire, même localement, qu'elle coïncide presque partout avec un homéomorphisme.
En effet, soit un point de continuité de et soit 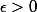tel que coïncide avec une fonction continue presque partout sur .
et coïncident forcément en tous les points de continuité de sans quoi l'ensemble contiendrait un petit intervalle et serait de mesure non nulle.
Soit un point de discontinuité de . On approxime par la gauche par une suite de points de continuité de et on a bien sur . De même, en approchant à droite par une suite de points de continuité de , on a et ceci contredit la continuité de en puisque par hypothèse.

Pour conclure, je dirai que l'énoncé de Rosie est purement ensembliste. Il ne suppose pas qu'on a contruit une mesure sur la tribu de Borel. Il faut donc y répondre sans employer l'expression "presque partout", à moins de montrer proprement que la mesure choisie est sans influence sur le résultat.

[El_Gato]

Par exemple la fonction "dédoublement des chiffres binaires" de [0,1[ dans lui-même (qui à .01011010001... par exemple associe .0011001111001100000011...) répond à ces critères. Ses points de discontinuité sont les nombres dont l'écriture binaire est finie. On peut facilement la prolonger à tout entier si on en a envie.

Salut,

Tu as raison j'ai fait une erreur: une application strictement croissante de IR dans IR n'est pas nécessairement un homéomorphisme local. Et merci pour ton (contre) exemple intéressant.

Autant pour moi.

Mais j'ai quand même l'impression qu'une application strictement monotone est bi-mesurable, ce qui résoudrait une fois pour toutes l'exercice de Rosie. A suivre...

[drj23]

si f est borelienne alors f(I) est mesurable pour tout intervalle I de la forme ]x,oo[, considere les intervalles I(n)=]a+1/n,oo[ tu vois que f[I(n)] et borelien ( car tt simplement I(n) est un ouvert) essaye de trouver une relation avec [a,oo[ et les I(n), et avec quelques proprités des mesures tu trouvera la solution.