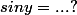Fonction arctan x
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cabaline
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Déc 2011, 13:21
-
 par cabaline » 16 Jan 2012, 12:24
par cabaline » 16 Jan 2012, 12:24
Bonjour, j'ai un exercice que je n'arrive pas à commencer : pour tout x dans R, montrer que arctan x = arcsin ( x/racine carré(1+x²))
J'ai du louper quelque chose car j'ai essayé avec tous les résultats connus de mon cours et je ne trouves pas.. si quelqu'un a une idée a me faire partager !
Merci
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 16 Jan 2012, 12:35
par Sylviel » 16 Jan 2012, 12:35
Une idée générale : écrire l'égalité sous forme de différence =0.
Ensuite il s'agit d'une égalité de fonctions compliquée, mais ayant une dérivée "simple"...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
JackeOLanterne
- Membre Relatif
- Messages: 333
- Enregistré le: 11 Nov 2010, 00:31
-
 par JackeOLanterne » 16 Jan 2012, 12:49
par JackeOLanterne » 16 Jan 2012, 12:49
Deux autres méthodes :
une analytique :
-
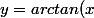 \Longleftrightarrow x= tan(y) = \frac{sin(y)}{...})
or

d'où :
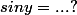
une géométrique :
- représenter l'arc dont la tangente est x sur un cercle trigonométrique et appliquer Pythagore.
-
cabaline
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Déc 2011, 13:21
-
 par cabaline » 16 Jan 2012, 18:53
par cabaline » 16 Jan 2012, 18:53
Merci de vos réponses, pour les dérivées, j'ai les deux dérivés de arctan x et arcsin x cependant, je ne vois pas le lien avec l'égalité.
Pour la deuxieme méthode (JackeOlanterne), cette exercice fait référence à un cours sur les dérivées, alros je ne sais pas si je peux vraiment l'utiliser..
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 16 Jan 2012, 18:56
par Sylviel » 16 Jan 2012, 18:56
Et bien tu veux montrer que h(x)=0 pour tout x.
Tu montres que h est dérivablen et que h'(x)=0.
Cela signifie que h est ...
Il ne reste plus qu'à ...
pour montrer que h(x) est toujours nulle.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
cabaline
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Déc 2011, 13:21
-
 par cabaline » 16 Jan 2012, 19:00
par cabaline » 16 Jan 2012, 19:00
Oui je comprends ça, mais je ne vois pas en quoi montrer cela, prouvera que arctan x = arcsin (x/racine carré 1+x²)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 16 Jan 2012, 19:04
par Sylviel » 16 Jan 2012, 19:04
Reprends ce que je t'ai dis :
écrire l'égalité sous forme de différence =0
puis
Et bien tu veux montrer que h(x)=0 pour tout x.
Tu montres que h est dérivable et que h'(x)=0.
Cela signifie que h est ...
Il ne reste plus qu'à ...
pour montrer que h(x) est toujours nulle.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
cabaline
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Déc 2011, 13:21
-
 par cabaline » 16 Jan 2012, 19:25
par cabaline » 16 Jan 2012, 19:25
J'ai mis sous forme de différence, j'ai dérivé la relation avec arctan x = 1/ 1+x² et arcsin (u(x)) = u'/ racine carrée (1+u²) et je trouve h'(x) = 1/1+x² - x²/racine carrée (1+x²) différent de 0 , ma dérivée est fausse.. les formules sont elles justes ou non?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 16 Jan 2012, 19:27
par Sylviel » 16 Jan 2012, 19:27
Les formules sont juste, mais que vaut ton u ? que vaut u' ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
cabaline
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Déc 2011, 13:21
-
 par cabaline » 16 Jan 2012, 19:43
par cabaline » 16 Jan 2012, 19:43
U(x) = x/racine carrée(1+x²)
u'(x) = x^3 /((racine carreé (1+x²)(1+x²)
deuxieme calcule : u'x = (x²-x+1)/(racine carrée1+x²)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 16 Jan 2012, 20:13
par Sylviel » 16 Jan 2012, 20:13
J'ai un doute sur ton calcul de dérivé de u...
Essaie de le refaire plus proprement.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
cabaline
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Déc 2011, 13:21
-
 par cabaline » 16 Jan 2012, 23:01
par cabaline » 16 Jan 2012, 23:01
Je trouve 1/ racine carrée (1+x²) j'ai refais mon calcule plusieurs fois e tj'ai toujours le même.. donc h'(x) ne s'annule pas et je ne sais plus quoi faire
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 16 Jan 2012, 23:30
par Sylviel » 16 Jan 2012, 23:30
pour u' ? Dans ce cas c'est bon si je ne m'abuses... je te rappelle que c'est la différence qu'il faut dériver (et je t'assure que la dérivée de la différence est bien nulle, donc si tu ne trouves pas 0 c'est que tu n'as pas dérivé proprement).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
cabaline
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Déc 2011, 13:21
-
 par cabaline » 17 Jan 2012, 12:22
par cabaline » 17 Jan 2012, 12:22
Bonjour, apres plusieurs calculs j'ai enfin trouvé la bonne dérivée, et h'(x) = 0 donc h(x) est constante = k. Or il faut donc montrer que k= 0 pour que l'égalité sois vérifié, et comment je fais ici pour que k=0?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Jan 2012, 12:53
par Sylviel » 17 Jan 2012, 12:53
essaie de calculer h(x) pour un x particulier.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Black Jack
 par Black Jack » 17 Jan 2012, 15:36
par Black Jack » 17 Jan 2012, 15:36
cabaline a écrit:Bonjour, apres plusieurs calculs j'ai enfin trouvé la bonne dérivée, et h'(x) = 0 donc h(x) est constante = k. Or il faut donc montrer que k= 0 pour que l'égalité sois vérifié, et comment je fais ici pour que k=0?
Calcule h(x) pour une valeur quelconque de x.
Tant qu'à faire, il faut se simplifier la vie et calculer h(0) = ...
Et puis conclure.
:zen:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Jan 2012, 15:37
par Sylviel » 17 Jan 2012, 15:37
Remarque : h(1) se calcule aussi...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
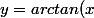 \Longleftrightarrow x= tan(y) = \frac{sin(y)}{...}) or
or  d'où :
d'où :