Factorisation polynome complexe
13 messages
- Page 1 sur 1
 Factorisation polynome complexe
Factorisation polynome complexe
Bonjour, Je suis actuellement en prépa et j'aurais besoin de votre aide pour répondre à ses questions s'il vous plait.
Je sais qu'il faut utiliser la factorisation d'un polynome complexe à l'aide de d'Alembert Gauss mais je n'arrive pas à trouver la solution du polynome
Enoncé:
Factoriser le polynome P = 1+X+...+X^(n-1) dans C[x] (->Complexe)
Pourriez vous m'aider s'il vous plait
la puissance (n-1) me gene
Je sais qu'il faut utiliser la factorisation d'un polynome complexe à l'aide de d'Alembert Gauss mais je n'arrive pas à trouver la solution du polynome
Enoncé:
Factoriser le polynome P = 1+X+...+X^(n-1) dans C[x] (->Complexe)
Pourriez vous m'aider s'il vous plait
la puissance (n-1) me gene
Re: Factorisation polynome complexe
salut
connais-tu les suites géométriques ?
connais-tu les suites géométriques ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Factorisation polynome complexe
zygomatique a écrit:salut
connais-tu les suites géométriques ?
Oui je connais les suites mais en quoi je peux l'utiliser?
Re: Factorisation polynome complexe
Archytas a écrit:Tu peux considérer (X-1)P, ça te mettras sur la voie !
veuillez m'excuser mais je ne comprends pas ce que vous voulez dire
Vous voulez dire que :
P=1+X+...+X^(n-1) deviendra quoi?
Re: Factorisation polynome complexe
Que peux tu dire de la somme d'une suite géométrique ?
Ma méthode revient un peu au même, je te demande de calculer le produit (X-1)*P.
Tu auras un polynôme que tu sais factoriser
Ma méthode revient un peu au même, je te demande de calculer le produit (X-1)*P.
Tu auras un polynôme que tu sais factoriser
Re: Factorisation polynome complexe
Archytas a écrit:Que peux tu dire de la somme d'une suite géométrique ?
Ma méthode revient un peu au même, je te demande de calculer le produit (X-1)*P.
Tu auras un polynôme que tu sais factoriser
la somme d'une suite géométrique est définie par:
si la raison q est différente de 1 alors : la somme d'une suite géométrique est: (1-q^(n+1))/(1-q)
Concernant votre méthode:
quand je calcule (X-1)P= (X+X^2+...+X^n)(1+X+...-X^(n-1)
si q=1 alors: (n+1)U0 avec U0 le premier terme
Re: Factorisation polynome complexe
Prepa_S a écrit:la somme d'une suite géométrique est: (1-q^(n+1))/(1-q)
A quelle suite géométrique pourrait on l'appliquer pour notre problème ?
Prepa_S a écrit:Concernant votre méthode:
quand je calcule (X-1)P= (X+X^2+...+X^n)(1+X+...-X^(n-1)
Un petit effort ...
Re: Factorisation polynome complexe
Archytas a écrit:Prepa_S a écrit:la somme d'une suite géométrique est: (1-q^(n+1))/(1-q)
A quelle suite géométrique pourrait on l'appliquer pour notre problème ? Prepa_S a écrit:Concernant votre méthode:
Prepa_S a écrit:Concernant votre méthode:
quand je calcule (X-1)P= (X+X^2+...+X^n)(1+X+...-X^(n-1)
Un petit effort ...
je vais y réflechir merci de votre aide
Re: Factorisation polynome complexe
1/ P(1) = ... ?? n'est pas nul donc 1 n'est pas racine de P
2/ donc pour tout x<> 1 ::
peut-être apprendre et retenir son cours de terminale ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Factorisation polynome complexe
Bonjour;
soit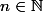 /{0,1}, pour factoriser
/{0,1}, pour factoriser  = 1 + \ldots+x^{n-1}) il faut d'abord - comme l'a dit M. Zygomatique - savoir que:
il faut d'abord - comme l'a dit M. Zygomatique - savoir que:
1) Les solutions de l'équation sont de la forme
sont de la forme  avec
avec 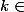 {0,
{0,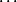 ,n-1} ;
,n-1} ;
2)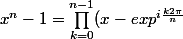 = (x-1) \prod_{k=1}^{n-1}(x- exp^{i\frac{k2\pi}{n}})) ;
;
donc pour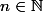 ,
,  = 1 + \ldots+x^{n-1} = \frac{x^n - 1}{ x - 1} = \dots) .
.
Un conseil d'un ami qui vient de passer le CNC cette année, il faut profiter de la période des vacances pour préparer dés maintenant le concours: l'année prochaine se termine fin Janvier et non fin Juin. Les mois de Février, Mars et avril sont pour les préparations intenses et les révisions de toutes les matières.
Bonne chance et bon courage et surtout ne baisse jamais les mains.
soit
1) Les solutions de l'équation
2)
donc pour
Un conseil d'un ami qui vient de passer le CNC cette année, il faut profiter de la période des vacances pour préparer dés maintenant le concours: l'année prochaine se termine fin Janvier et non fin Juin. Les mois de Février, Mars et avril sont pour les préparations intenses et les révisions de toutes les matières.
Bonne chance et bon courage et surtout ne baisse jamais les mains.
Re: Factorisation polynome complexe
zygomatique a écrit:
1/ P(1) = ... ?? n'est pas nul donc 1 n'est pas racine de P
2/ donc pour tout x<> 1 ::
peut-être apprendre et retenir son cours de terminale ...
merci à vous
Re: Factorisation polynome complexe
aymanemaysae a écrit:Bonjour;
soit/{0,1}, pour factoriser
il faut d'abord - comme l'a dit M. Zygomatique - savoir que:
1) Les solutions de l'équationsont de la forme
avec
{0,
,n-1} ;
2);
donc pour,
.
Un conseil d'un ami qui vient de passer le CNC cette année, il faut profiter de la période des vacances pour préparer dés maintenant le concours: l'année prochaine se termine fin Janvier et non fin Juin. Les mois de Février, Mars et avril sont pour les préparations intenses et les révisions de toutes les matières.
Bonne chance et bon courage et surtout ne baisse jamais les mains.
Bonjour
je tenais à vous remercier du fond du coeur pour votre conseil et vos encouragements... il m'arrive de baisser les bras, votre message me touche énormément. Merci encore c'est très aimable de votre part. Concernant les révisions, je compte réviser et revoir mes lacunes pendant les vacances.
merci
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
