Expression d'une suite

[MAC52]

Bonjour, je suis en terminale S et je voulais savoir si l'on pouvait exprimer en fonction de n la suite (Un) définie sur N* par:
u(1)=0
et u(n+1)=V(2+u(n)) (désolé, je ne sais pas écrire en Latex)
(il est facile de montrer qu'elle est bien définie sur N*, soit.)
En fait, je m'adresse à ceux du supérieur car je ne crois pas qu'on voit ce genre de suites en Tle, de plus cette suite m'intéresse car il est "facile" de démontrer que, pour tout entier naturel n non-nul:
cos(Pi/(2^n))=u(n)/2. (grâce à la récurrence et à la formule de duplication du cosinus)
Certes, ça n'a peut-être pas trop d'intérêt, mais je serais intéressé de savoir s'il était possible de simplifier la suite (Un).

MAC

[yos]

Tu donnes toi-même la réponse : .
Plus simple, je sais pas ce qu'il te faut.

[MAC52]

Oui, mais le but premier était justement de calculer les cosinus des réels Pi/(2^n).
Il serait assez long de simplifier u(10), par exemple, pour trouver cos(Pi/1024).
Au fait, existe-t-il une manière de "simplifier" l'écriture de cos(x) ? (tout comme le fait la calculatrice pour la fonction exponentielle, qu'elle approche avec une fonction polynôme)

[yos]

Justement. Ta suite permet de donner des valeurs (exactes) sous formes de radicaux de . Les radicaux sont un peu empilés mais on peut pas faire mieux.
Si on pouvait écrire cos x avec des fonctions plus simples que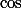 , ça se saurait.
Il y a bien la somme infinie des qui est égale à cos x mais c'est pas ce qu'on peut appeler "plus simple".

[MAC52]

C'est marrant, j'avais déjà réussi à écrire cosinus sous cette forme, mais j'avais laissé tomber, car ça ne semblait vraiment pas égal.
Enfin bon, ça n'est pas grave, merci pour ta réponse.