Déterminer l'expression d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 01 Juil 2013, 10:29
par Romanouch » 01 Juil 2013, 10:29
Bonjour,
Je ne vois pas comment faire pour déterminer l'expression de la suite suivante, définie par:
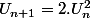
Quelqu'un peut-il me donner une piste?
Merci par avance.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 01 Juil 2013, 10:31
par XENSECP » 01 Juil 2013, 10:31
Tu as une valeur initiale?
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 01 Juil 2013, 10:40
par Romanouch » 01 Juil 2013, 10:40
XENSECP a écrit:Tu as une valeur initiale?
Oui:
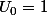

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 01 Juil 2013, 10:59
par capitaine nuggets » 01 Juil 2013, 10:59
Salut !
Romanouch a écrit:Bonjour,
Je ne vois pas comment faire pour déterminer l'expression de la suite suivante, définie par:
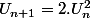
Quelqu'un peut-il me donner une piste?
Merci par avance.
Soit tu pars de l'expression de

:
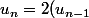^2)
et
^2)
donc
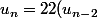^2\)^2=2^3 (u_{n-2})^4)
.
Ensuite,
^2)
donc
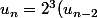^4=...)
et ainsi de suite.
Tu peux alors conjecturer

en fonction de

et démontrer ta conjecture par récurrence :++:
Soit tu pars de

:
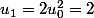
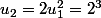
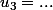
etc
-
spike0789
- Membre Relatif
- Messages: 131
- Enregistré le: 06 Mai 2013, 10:50
-
 par spike0789 » 01 Juil 2013, 11:00
par spike0789 » 01 Juil 2013, 11:00
Salut,
L'idée que j'ai eu, c'est d'écrire les relations entre U(n+1), U(n), U(n-1), de conjecturer l'expression et de conclure par récurrence.
On voit que U(n+1)=2*U(n)^2=2*4*(U(n-1))^4. En continuant, on voit qu'on a le produit 2*4*8*... donc le produit pour k allant de 0 à n de 2^(2^k).
J'espère que ca te met sur la voie (et en espérant que je n'ai pas fait d'erreurs bien sur)
-
spike0789
- Membre Relatif
- Messages: 131
- Enregistré le: 06 Mai 2013, 10:50
-
 par spike0789 » 01 Juil 2013, 11:23
par spike0789 » 01 Juil 2013, 11:23
Sinon une méthode plus rapide serait de faire :
On a
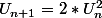
, donc en passant au logarithme (en s'assurant préalablement que Un>0)
ln
-
spike0789
- Membre Relatif
- Messages: 131
- Enregistré le: 06 Mai 2013, 10:50
-
 par spike0789 » 01 Juil 2013, 11:24
par spike0789 » 01 Juil 2013, 11:24
=ln(2)+2ln(U_n))
En ajoutant ln(2) de chaque côté :
=2ln(2U_n))
Donc une suite géométrique ...
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 01 Juil 2013, 12:54
par kasmath » 01 Juil 2013, 12:54
spike0789 a écrit:=ln(2)+2ln(U_n))
En ajoutant ln(2) de chaque côté :
=2ln(2U_n))
Donc une suite géométrique ...
Bonne répense , mais il faut montrer par récurrence que

c'est évident ! mais il faut le prouvé
-
spike0789
- Membre Relatif
- Messages: 131
- Enregistré le: 06 Mai 2013, 10:50
-
 par spike0789 » 01 Juil 2013, 13:01
par spike0789 » 01 Juil 2013, 13:01
kasmath a écrit:Bonne répense , mais il faut montrer par récurrence que

c'est évident ! mais il faut le prouvé
Oui en effet, c'est la 1ere étape
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 01 Juil 2013, 13:04
par Romanouch » 01 Juil 2013, 13:04
Merci pour vos réponses. J'oublie souvent d'essayer de trouver "à tâtons".
En passant par le logarithme, c'est encore mieux je trouve!
Merci à vous.
Je trouve
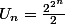
A la prochaine.
-
spike0789
- Membre Relatif
- Messages: 131
- Enregistré le: 06 Mai 2013, 10:50
-
 par spike0789 » 01 Juil 2013, 13:09
par spike0789 » 01 Juil 2013, 13:09
C'est bien la bonne réponse
A +
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 01 Juil 2013, 17:03
par deltab » 01 Juil 2013, 17:03
Bonjour à tous
On peut même généraliser pour
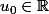
(ou même

):
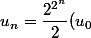^{2^{n-1}})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités