Bonjour à tous
Pourriez vous avoir l'amabilité de donner votre avis sur le problème posé par ce fil .
http://www.forum.math.ulg.ac.be/viewthr ... 0&id=61527
Expression par radicaux de la racine cubique d'un complexe
8 messages
- Page 1 sur 1
Re: expression par radicaux de la racine cubique d'un comple
Bonjour,
 est solution de l'équation
est solution de l'équation
*x^6 + (-15*a^2 - 27*b^2)*x^3 + (-a^3)=0)
C'est une équation du troisième degré en , Donc
, Donc  s'exprime bien en fonction de
s'exprime bien en fonction de  et
et  au moyen de racines carrées et cubiques.
au moyen de racines carrées et cubiques.
Après, on a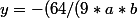*x^7 - 56/(9*b)*x^4 + (-8*a^2 - 27*b^2)/(9*a*b)*x)) .
.
C'est une équation du troisième degré en
Après, on a
Re: expression par radicaux de la racine cubique d'un comple
Bonsoir Gabuzomeu et merci pour ta sollicitude.
Ce que nous aimerions alors , c'est d'avoir au moins une formule pour X sans boucler sur une nouvelle racine cubique d'un nombre complexe .
Ce que nous aimerions alors , c'est d'avoir au moins une formule pour X sans boucler sur une nouvelle racine cubique d'un nombre complexe .
Re: expression par radicaux de la racine cubique d'un comple
Le discriminant de l'équation unitaire de degré 3 en  est
est  * b^2 * (a^2 + b^2)^2>0) (on suppose
(on suppose 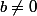 , n'est-ce pas ?). Toutes ses racines sont donc réelles. On ne prend donc que des racines cubiques de nombres réels.
, n'est-ce pas ?). Toutes ses racines sont donc réelles. On ne prend donc que des racines cubiques de nombres réels.
Re: expression par radicaux de la racine cubique d'un comple
Encore merci
Je dois donc réviser
Je te recontacterais
Je dois donc réviser
Je te recontacterais
Re: expression par radicaux de la racine cubique d'un comple
OK je vois, les formules de Cardan passent par des racines cubiques de nombres complexes. Tu ne veux que des racines de nombres réels (c'est donc autre chose que résoudre par radicaux).
Re: expression par radicaux de la racine cubique d'un comple
Bonjour
En langage mathématique la question est:
L' équation du troisième degré est elle résoluble dans une extension radicale de incluse dans
incluse dans  lorqu'elle admet trois racines réelles?
lorqu'elle admet trois racines réelles?
En langage mathématique la question est:
L' équation du troisième degré est elle résoluble dans une extension radicale de
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
