Salut !
Roby a écrit:Bonjour je m'entraine a faire des exo sur les matrices et je suis tombé sur un exercice avec des questions relative aux exponentielles , ce qui ne me parle pas trop .
Je sais que l'exponentiel de x c'est :
exp(x)=
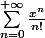
= 1 + x +

Et que pour une matrice c'est la même chose mais avec une matrice en guise de x
exp(M)=
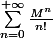
= Id + M +

Je ne m'y connais pas en exponentiel mais si on me demande exp(3) comment je le calcul ? Je veux dire par là : à quelle valeur de n je m’arrête ?
Cette définition de l'exponentielle d'une matrice est donnée sous forme d'une série : il y a une infinité (dénombrable) de termes, donc tu ne t'arrêtes jamais ! Si tu as un doutes concernant la formule, regarde ce qui se passe dans le cas de l'exponentielle d'un réel

Roby a écrit:Cela fait voici la vrai question
Soit D une matrice diagonale. Calculer exp(D).
En cherchant sur le net j'ai trouvé que pour une matrice diagonale il suffit de faire l'exponentiel de chaque élément de la diagonale .
Mais je ne vois pas quoi répondre à la question...
Est ce que le fait qu'elle soit diagonale permet de simplifier l'équation ?
Plaçons nous sur l'ensemble
)
des matrices carrées d'ordre

à coefficient dans
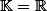
ou

et considérons une matrice diagonale quelconque de cet ensemble
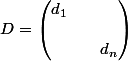
. Tu peux alors par exemple montrer (sans réelle difficulté) à l'aide d'un raisonnement par récurrence sur
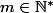
que
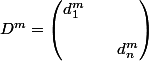
.
Du coup, si tu as une matrice diagonale

(ou une matrice diagonalisable

i.e. il existe donc

tel que

), tu as :
=\sum_{m = 0}^{+\infty} \frac{D^m}{m!}=\sum_{m = 0}^{+\infty} \frac{1}{m!} \begin{pmatrix} d_1^m & & \\ & & \\ & & d_n^m \end{pmatrix}=\begin{pmatrix} \sum_{m = 0}^{+\infty} \frac{1}{m!}d_1^m & & \\ & & \\ & & \sum_{m = 0}^{+\infty} \frac{1}{m!}d_n^m \end{pmatrix} =\begin{pmatrix} e^{d_1} & & \\ & & \\ & & e^{d_n} \end{pmatrix})
Dans le cas où on a

, il suffit de remarquer que pour tout
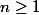
:
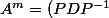^m = (PDP^{-1})(PDP^{-1})...(PDP^{-1})=PD(P^{-1}P)D(P^{-1}P)D(P^{-1}P)...(P^{-1}P)DP^{-1}=PD^mP^{-1})
Le reste des calculs restent globalement identiques pour avoir
 = P\exp(D) P^{-1})
.
Le fait que la matrice dont on cherche l'exponentielle soit diagonale/diagonalisable est la partie la plus simple du calcul d'exponentielles de matrices. Par exemple, la matrice

n'est pas diagonalisable mais on peut montrer facilement qu'elle est nilpotente (i.e. il existe un entier
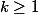
tel que pour tout
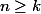
,
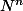
est la matrice nulle) donc la série définissant l'exponentielle de N contiendra un nombre fini de termes, donc on pour la calculer directement. Sinon, la matrice
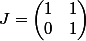
n'est pas diagonalisable donc pour calculer son exponentielle, il faut aller un peu plus loin, mais je ne vais pas m'attarder dessus, ce n'est pas le sujet de ta question.
Roby a écrit:Soit M une matrice diagonalisable de matrice diagonale D. Exprimer M^n, puis en utilisant cette expres-
sion, donner une expression pour exp(M) en fonction de exp(D).
En cherchant sur le net :
Ici si M est diagonale alors je sais qu' élever une matrice diagonale D à une certaine puissance revient à élever les coefficients de la diagonale de D à cette puissance
Mais je suis un peu perdu ... Si quelqu'un arrive a m'éclairer je lui en serai fortement reconnaissant.
Merci !
Voir ce que j'ai écrit précédemment.
@+

