DL exponentielle complexe
28 messages
- Page 1 sur 2 - 1, 2
DL exponentielle complexe
Bonjour,
peut on faire un DL d'une exponentielle complexe?
Ca marche pareil qu'une exponentielle réelle?
Merci
edit: I mean e^(ix)~1+ix
peut on faire un DL d'une exponentielle complexe?
Ca marche pareil qu'une exponentielle réelle?
Merci
edit: I mean e^(ix)~1+ix
Tu ne sais rien sur les exponentielles complexes, tu dois tout redémontrer ^^
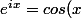 + isin(x))
Donc je suppose qu'en ayant un développement limité de cos(x) et sin(x) en zéro, on doit bien pouvoir retrouver que
^n \frac{x^{2n}}{(2n)!} +i (-1)^n \frac{x^{2n+1}}{(2n+1)!} + o(x^{2n+1}))
Donc ça ne marche pas tout à fait comme une exponentielle normal, vu qu'apparaissent deux moins sur quatre...
Sinon on peut essayer avec la formule de Taylor-Young, mais alors là bon courage, et surtout, sans moi !
Donc je suppose qu'en ayant un développement limité de cos(x) et sin(x) en zéro, on doit bien pouvoir retrouver que
Donc ça ne marche pas tout à fait comme une exponentielle normal, vu qu'apparaissent deux moins sur quatre...
Sinon on peut essayer avec la formule de Taylor-Young, mais alors là bon courage, et surtout, sans moi !
miikou a écrit:attention a la somme de DL ..
Je peux additionner des DL comme je veux, ce sont les équivalents que je n'ai pas droit de sommer sans justifications, à cause des termes qui pourraient éventuellement s'annuler...
Le problème des DL, c'est quand on les compose, mais là je ne vois pas où je fais une telle opération...
Au pire vous pouvez demander à un logiciel de calcul formel...
Mais ><
Nan, un équivalent est le premier, voire les deux premiers termes d'un DL.
Un DL est un polynôme infini. Il s'obtient à partir de la formule de Taylor-Young appliqué à la fonction en un point.
Si f et g possèdent deux D.L.n, alors f + g possède un D.L.n qui s'obtient en effectuant la somme des deux polynômes.
Là chaque DL a soit des termes de puissances paires, soit des termes de puissances impaires, et ils s'arrêtent tous les deux à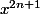 donc je vois pas le problème avec cette addition de DL ?!
donc je vois pas le problème avec cette addition de DL ?!
Si j'étais parti de la forme d' en remplaçant x par ix, là j'aurais compris que tu hurles au scandale, vu que j'aurais été bien embêté pour justifier une telle composition de DL... mais ce n'est pas le cas !
en remplaçant x par ix, là j'aurais compris que tu hurles au scandale, vu que j'aurais été bien embêté pour justifier une telle composition de DL... mais ce n'est pas le cas !
Alors si tu vois une erreur de ma part, tu m'expliques clairement laquelle, je serai heureux de progresser, et je serai prompt à reconnaitre que je me suis trompé...
Edit : -_-"
Nan, un équivalent est le premier, voire les deux premiers termes d'un DL.
Un DL est un polynôme infini. Il s'obtient à partir de la formule de Taylor-Young appliqué à la fonction en un point.
Si f et g possèdent deux D.L.n, alors f + g possède un D.L.n qui s'obtient en effectuant la somme des deux polynômes.
Là chaque DL a soit des termes de puissances paires, soit des termes de puissances impaires, et ils s'arrêtent tous les deux à
Si j'étais parti de la forme d'
Alors si tu vois une erreur de ma part, tu m'expliques clairement laquelle, je serai heureux de progresser, et je serai prompt à reconnaitre que je me suis trompé...
Edit : -_-"
wapita a écrit:edit: I mean e^(ix)~1+ix
ATTENTION : c'est une erreur classique de croire que e^(ix)~1+ix signifie davantage que e^(ix)~1 : en effet 1+ix ~1 ~1+3x² ...
Donc on peut écrire aussi e^(ix)~1+3x^2 sans commettre de faute !
En fait, il faut écrire e^(ix) - 1 ~ ix : ça c'est plus précis que e^(ix)~1 :id:
Shaolan a écrit:Tu ne sais rien sur les exponentielles complexes, tu dois tout redémontrer ^^
Donc je suppose qu'en ayant un développement limité de cos(x) et sin(x) en zéro, on doit bien pouvoir retrouver que
Donc ça ne marche pas tout à fait comme une exponentielle normal, vu qu'apparaissent deux moins sur quatre...
Ben si, c'est exactement pareil :
e^x = 1 + x + x²/2 + ...
e^(ix) = 1 + x + (ix)²/2 + ...
les moins que tu remarques proviennent des puissances du coefficient complexe i dans (ix)
Shaolan a écrit:Sinon on peut essayer avec la formule de Taylor-Young, mais alors là bon courage, et surtout, sans moi !
La formule de Taylor pour l'exponentielle est évidente puisque la fonction exponentielle se dérive à vu d'oeil !
Shaolan a écrit:Je peux additionner des DL comme je veux, ce sont les équivalents que je n'ai pas droit de sommer sans justifications, à cause des termes qui pourraient éventuellement s'annuler...
Le problème des DL, c'est quand on les compose, mais là je ne vois pas où je fais une telle opération...
Personnellement, j'aime bien les DL (même avec un seul terme avant un petit o) car ils permettent de manipuler des égalités en toute confiance. Calculs un peu plus lourds, certes... (on ne peut pas gagner sur tous les tableaux)
Shaolan a écrit:Au pire vous pouvez demander à un logiciel de calcul formel...
Faut pas se priver, c'est sûr ! :zen:
"Leon1789" a écrit:Ben si, c'est exactement pareil : e^x = 1 + x + x²/2 + ... e^(ix) = 1 + x + (ix)²/2 + ...
les moins que tu remarques proviennent des puissances du coefficient complexe i dans (ix)
Oui, je m'en suis rendu compte après :$
Mais je suppose que le démontrer à partir de l'exponentiel est faux ? à cause d'une composition, il vaut mieux repasser à la forme cos + isin comme je l'ai fait, nan ?
"Leon1789" a écrit:La formule de Taylor pour l'exponentielle est évidente puisque la fonction exponentielle se dérive à vu d'oeil !
Je ne dis pas forcément que ça va etre compliqué, je dis sans moi parce que j'ai horreur de la formule de Taylor-Young et que je ne la retiens jamais correctement XD
Shaolan a écrit:Nan, un équivalent est le premier, voire les deux premiers termes d'un DL.
Un DL est un polynôme infini. Il s'obtient à partir de la formule de Taylor-Young appliqué à la fonction en un point.
oula !
d'une, un équivalent est essentiellement le premier terme non nul (sauf les cas exceptionnelle de la fonction nulle) du DL. Après on peut ajouter n'importe qu'elle expression négligeable, ça reste équivalent. (cf e^x ~ 1 + x ~ 1-10.x^2)
Et puis un DL n'est pas un polynôme infini (au passage, polynome infini = série entière), parce qu'un DL possède un ordre, qui est un majorant (souvent égal) au degré de la partie polynomial du DL (sans parler du reste du DL)
Shaolan a écrit:Si j'étais parti de la forme d'en remplaçant x par ix, là j'aurais compris que tu hurles au scandale, vu que j'aurais été bien embêté pour justifier une telle composition de DL... mais ce n'est pas le cas !
ben nan, moi, je n'aurais pas hurlé puisque c'est correct :zen:
(nos messages se croisent..)
Shaolan a écrit:Mais je suppose que le démontrer à partir de l'exponentiel est faux ? à cause d'une composition, il vaut mieux repasser à la forme cos + isin comme je l'ai fait, nan ?
Tout dépend de la définition de l'exp complexe que l'on prends... c'est toujours le même problème.
Shaolan a écrit:Je ne dis pas forcément que ça va etre compliqué, je dis sans moi parce que j'ai horreur de la formule de Taylor-Young et que je ne la retiens jamais correctement XD
C'est vrai que, dans le cadre des DL d'une fonction "compliquée", la formule de Taylor-Young n'est pas très utile en général car c'est souvent laborieux de dériver 3 ou 4 fois.
Je crois aussi qu'il vaut mieux connaitre les DL des quelques fonctions usuelles et de savoir comme manipuler les DL pour obtenir celui d'une fonction donnée.
"Leon1789" a écrit:Et puis un DL n'est pas un polynôme infini (au passage, polynome infini = série entière), parce qu'un DL possède un ordre, qui est un majorant (souvent égal) au degré de la partie polynomial du DL (sans parler du reste du DL)
Oui, je confond un peu les deux -_-" merci de la précision =D
"Leon1789" a écrit:d'une, un équivalent est essentiellement le premier terme non nul (sauf les cas exceptionnelle de la fonction nulle) du DL. Après on peut ajouter n'importe qu'elle expression négligeable, ça reste équivalent. (cf e^x ~ 1 + x ~ 1-10.x^2)
Je me suis mal exprimé, je voulais dire que l'on utilisais bien souvent que le premier ou les deux premiers (et là je pense à cos) dans les équivalent. Évidemment on peut aller plus loin...
"Leon1789" a écrit:ben nan, moi, je n'aurais pas hurlé puisque c'est correct
Tu veux dire que l'on peut remplacer directement x par ix ?! ma prof nous répète tout le temps que l'on n'a pas de résultats là dessus, et qu'il faut redémontrer...
Je pense par exemple à ceci :
Mais il faut redémontrer à partir des arguments et modules que
Donc je préfère vraiment redémontrer à chaque fois...
Shaolan a écrit:Oui, je confond un peu les deux -_-" merci de la précision =D
juste en passant, un truc amusant :
une fonction est toujours égale à son DL (en tout ordre) à cause du reste,
mais une fonction n'est pas toujours égale à son "DL infini" !
Attention aux sommes infinies.. :zen:
Shaolan a écrit:Je me suis mal exprimé, je voulais dire que l'on utilisais bien souvent que le premier ou les deux premiers (et là je pense à cos) dans les équivalent. Évidemment on peut aller plus loin...
je ne comprends pas trop ce que tu veux dire, mais je voudrais juste préciser ceci :
si l'information cos(x) ~ 1 n'est pas suffisante pour conclure une démo, mais qu'en utilisant cos(x) ~ 1-x²/2 on arrive à conclure, alors la démo est fausse !
...car cos(x) ~ 1-x²/2 ne signifie rien de plus que cos(x) ~ 1 :dodo:
Shaolan a écrit:Tu veux dire que l'on peut remplacer directement x par ix ?! ma prof nous répète tout le temps que l'on n'a pas de résultats là dessus, et qu'il faut redémontrer...
(...)
Donc je préfère vraiment redémontrer à chaque fois...
tu as raison : certains résultats ne sont pas acceptés à certains niveaux, mais tout à fait habituels à d'autre. Exemple, j'imagine qu'en première, on n'admet pas qu'un étudiant balance les solutions d'une équation de degré 2 sans preuve... alors qu'en Master 2, cela ne pose pas de problème évidemment. Tout est une question de niveau d'exigence. Il faut donc respecter l'exigence de ses profs, c'est clair.
28 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
