bonjour je dois trouver les couple (a,b) de N² tels que a^b=b^a . Je suis complètement bloqué a part écrire sous forme exponentielle je ne vois pas quoi faire !
Merci de votre aide
Exo sup
6 messages
- Page 1 sur 1
Il y a une solution évidente  , les solutions a=b, et je crois que ce sont les seules, mais c'est moins facile à prouver (on peut montrer que a et b ont forcément les mêmes facteurs premiers, par exemple, puis en supposant
, les solutions a=b, et je crois que ce sont les seules, mais c'est moins facile à prouver (on peut montrer que a et b ont forcément les mêmes facteurs premiers, par exemple, puis en supposant 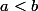 , écrire
, écrire ^a) et prouver qu'aucune puissance d'un rationnel strict ne donne un entier. Ca entraine que
et prouver qu'aucune puissance d'un rationnel strict ne donne un entier. Ca entraine que  est entier, donc que
est entier, donc que 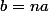 et on s'en tire (en fait, on va prover que b est forcément une puissance de a)
et on s'en tire (en fait, on va prover que b est forcément une puissance de a)
matthaw
exact je trouve seulement le couple (2,4) mais ma démo est plutot bancale !
c'est un exo posé a l'X , pas facile pour un sup :d
c'est un exo posé a l'X , pas facile pour un sup :d
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
