Bonjour à tous,
je bloque sur un exercice dont voici l'énoncé:
a un nbre complexe non nul, n et m 2entiers naturels>0
Montrer que pgcd(X^n -a^n , X^m - a^m)= X^r - a^r
où r=pgcd(m,n)
voilà.
j'ai commencé par décomposer ces polynômes en produits de facteurs irréductibles. je me suis dit qu'ils ont r facteurs en commun. j'ai écrit a sous forme exponentielle et j'ai essayé de trouver une relation liant m et n mais avec celle-ci je n'aboutit à rien. bref,je ne vois pas comment introduire ce r=pgcd(m,n).. :hein:
si vous pouviez m'aider,me donner quelques indices... je vous en serais très reconnaissante.merci
:++:
Exo:pgcd de polynômes ds C[X]...
6 messages
- Page 1 sur 1
Il faut analyser les polynômes de la forme =x^{S-1}+x^{S-2}a+...+x^{1}a^{S-2}+a^{S-1}) . Il faut remarquer que
. Il faut remarquer que =(x^S-a^S)/(x-a)) quand
quand 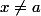 , mais
, mais /(x-a)) s'anulle si et seulement si
s'anulle si et seulement si  . Remarquer que
. Remarquer que =Sa^{S-1}\neq 0)
Soient sont lequels qui apparaîtent dans le message de QUIDAM. On va montrer que
sont lequels qui apparaîtent dans le message de QUIDAM. On va montrer que ) et
et ) n'ont pas de racines communes.
n'ont pas de racines communes.
Si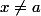
 et
et  est impossible, parce qu'on aurait que
est impossible, parce qu'on aurait que  et
et  , où
, où 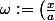) . Comme
. Comme =1) , il existe
, il existe  tels que
tels que  . Alors
. Alors 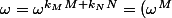^{k_M}(\omega^N)^{k_N}=1.1=1) , celui-là est une contradiction.
, celui-là est une contradiction.
Maitenant analyse=\sum_{i=0}^{n-1} [(X^r)^i(a^r)^{n-1-i}]) et
et =\sum_{i=0}^{m-1} [(X^r)^i(a^r)^{m-1-i}])
Soient
Si
Maitenant analyse
Quitte à passer par les racines, autant le faire dés le début de l'exo. C'est d'ailleurs suggéré par l'énoncé qui se place dans C[X] alors que le résultat est vrai sur Q[X] ou R[X] par exemple.
On peut dire que les racines de sont les complexes
sont les complexes 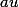 où u décrit les racines m-ème de l'unité . On fait pareil pour
où u décrit les racines m-ème de l'unité . On fait pareil pour 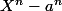 et on cherche les racines communes à ces deux polynômes : ce sont clairement les complexes
et on cherche les racines communes à ces deux polynômes : ce sont clairement les complexes  où w décrit les racines de l'unité d'ordre m et n à la fois , c'est à dire celles d'ordre r.
où w décrit les racines de l'unité d'ordre m et n à la fois , c'est à dire celles d'ordre r.
On peut dire que les racines de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
