Existence d'une suite

[ilikoko123]

salut à tous
une petite question d'un problème me bloque, j'aimerais que vous m'aidiez
montrer qu'il existe une suite réelle an ayant la propriété suivante :
pour tout p dans N* , pour tout intervalle I non réduit à un point et pour toute fonction complexe f de classe C(infini) sur I la fonction g définie par :
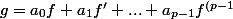vérifie

avec les sont des coefficients independants de f qu'on ne cherche pas à calculer
merci de votre aide

[JaCQZz]

Si est définie telle que plus haut, alors il manque le coefficient devant lors du passage à la dérivée :
Quant au développement en série, essaie de trouver une relation de récurrence entre : et où

[ilikoko123]

le est = 1 en fait c'est demandé après
quant au reste je me demande si ça necessite connaitre le developpement en série des fonctions ? car n l'a pas encore fait :/

[Robot]

Absolument pas.
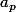
Il y a juste à voir que si on connaît des pour qui marchent, alors on trouve facilement un qui marche. Il suffit d'écrire ce qu'on demande à .

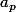
[ilikoko123]

tu veut dire qu'on construira cette suite par récurrence hein ?

[Robot]

Ouaip.....

[JaCQZz]

tu veut dire qu'on construira cette suite par récurrence hein ?

Que donne la construction de la suite ? Fais-le à l'ordre 1 puis prouve-le par hérédité en supposant l'expression vraie pour