Bonjour,
J'ai fait deux exercices sur la méthode de Horner et j'aimerais savoir s'ils sont justes.
http://www.noelshack.com/2022-09-3-1646 ... 161043.jpg
http://www.noelshack.com/2022-09-3-1646 ... 161059.jpg
http://www.noelshack.com/2022-09-3-1646 ... 2-et-3.png
Exercices sur la méthode de Horner.
12 messages
- Page 1 sur 1
Re: Exercices sur la méthode de Horner.
Bonsoir Lisa,
pour les résultats d'Exo 3 annales:
je trouve pour Q1 en développant:
(x^2+x-12))
pour Q3, c'est ok
Pour Q4:
(x^2-4x+3))
pour Q4, la racine du polynôme P est -4 donc on factorise par (x+4)
Pour le résultat de l'exercice 2:
(x^2-5)-4)
On peut vérifier les factorisations obtenues en développant les résultats.
pour les résultats d'Exo 3 annales:
je trouve pour Q1 en développant:
pour Q3, c'est ok
Pour Q4:
pour Q4, la racine du polynôme P est -4 donc on factorise par (x+4)
Pour le résultat de l'exercice 2:
On peut vérifier les factorisations obtenues en développant les résultats.
Re: Exercices sur la méthode de Horner.
Coucou @mathelot,
Pour Q1 oui du coup j'ai vu mon erreur.
Pour Q3, je ne comprends pas. Si on reprend mon tableau :
-On descend 1. 1 fois 4 fait 4.
-On met 4 sous 0. 0 plus 4 fait 4. 4 fois 4 fait 16.
-On met 16 sous -13. -13+16 fait 3 d'ailleurs. 3 fois 4 fait 12.
-On met 12 sous 12. 12 plus 12 fait 24 qui est le reste.
On a donc :
(x-4)(1Xcarré + 4X + 3) + 24 non ?
D'ailleurs, je ne comprends pas pourquoi tu dis que -4 est racine de Q4 donc on factorise par (X-4) ?
Dans Q1 -1 était racine et on a factorisé par (X-1) non ?
Pour l'exercice deux oui j'ai vu je me suis trompée le reste est - 4 donc Q(3)=0 non ?
Pour Q1 oui du coup j'ai vu mon erreur.
Pour Q3, je ne comprends pas. Si on reprend mon tableau :
-On descend 1. 1 fois 4 fait 4.
-On met 4 sous 0. 0 plus 4 fait 4. 4 fois 4 fait 16.
-On met 16 sous -13. -13+16 fait 3 d'ailleurs. 3 fois 4 fait 12.
-On met 12 sous 12. 12 plus 12 fait 24 qui est le reste.
On a donc :
(x-4)(1Xcarré + 4X + 3) + 24 non ?
D'ailleurs, je ne comprends pas pourquoi tu dis que -4 est racine de Q4 donc on factorise par (X-4) ?
Dans Q1 -1 était racine et on a factorisé par (X-1) non ?
Pour l'exercice deux oui j'ai vu je me suis trompée le reste est - 4 donc Q(3)=0 non ?
Re: Exercices sur la méthode de Horner.
re,
Exercice 2, question 1
le dernier chiffre de ton résultat,i.e, le reste , est erroné.
On doit avoir

d'où=X^3-2X^2-5X+6=(X-2)(X^2-5)+(-4)=(X-2)(X^2-5)-4)
Exercice 2, question 2
Le reste de la division de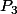 par
par 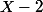 est
est ) ,i.e,
,i.e, =-4)
Exercice 2, question 3

Le reste de la division de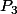 par
par 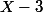 vaut 0.
vaut 0. 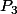 est divisible par
est divisible par 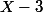
en effet, d'après le tableau:
=X^3-2X^2-5X+6=(X-3)(X^2+X-2) \textrm{ et le reste est nul})
d'où=0) . C'est le reste de la division de
. C'est le reste de la division de 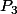 par
par 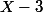 .
.
Exercice 2, question 1
le dernier chiffre de ton résultat,i.e, le reste , est erroné.
On doit avoir
d'où
Exercice 2, question 2
Le reste de la division de
Exercice 2, question 3
Le reste de la division de
en effet, d'après le tableau:
d'où
Re: Exercices sur la méthode de Horner.
On a le cours de la méthode de Horner sous Wikipédia à l'adresse:
https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Ruffini-Horner#:~:text=Elle%20pr%C3%A9sente%20un%20algorithme%20simple,une%20racine%20d'un%20polyn%C3%B4me.
pour nous aider.
On peut lire les paragraphes:
Valeur d'un polynôme en un point
Quotient d'un polynôme par X - x0
Dérivées successives de P en x0
https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Ruffini-Horner#:~:text=Elle%20pr%C3%A9sente%20un%20algorithme%20simple,une%20racine%20d'un%20polyn%C3%B4me.
pour nous aider.
On peut lire les paragraphes:
Valeur d'un polynôme en un point
Quotient d'un polynôme par X - x0
Dérivées successives de P en x0
Modifié en dernier par mathelot le 03 Mar 2022, 18:16, modifié 1 fois.
Re: Exercices sur la méthode de Horner.
Exercice 3 question 1
On doit calculer P'(1) avec la méthode de Horner, donc sans dériver le polynôme. La méthode indiquée par Wiki est assez longue et un peu difficile, je la reporte en fin de notre conversation.
Exercice 3 question 1 (suite)
Calcul de=\dfrac{P(X)}{X-1})
en X=1, il vient le tableau

Le reste de la division de P par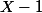 est nul. P est divisible par
est nul. P est divisible par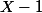 ; il vient
; il vient
=X^3-13X+12=(X-1)(X^2+X-12))
tu as une erreur sur le polynôme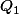 (X)
(X)
Le reste de la division , égal à P(1),est nul.
Ta notation=(X-1)(X^2+X-12)) est erronée.
est erronée.
Il faut écrire:
=X^2+X-12)
et=(X-1)(X^2+X-12))
Exercice 3 question 2
Calcul de=\dfrac{P(X)}{X-3})
en X=3, il vient le tableau

Le reste de la division de P par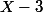 est nul. P est divisible par
est nul. P est divisible par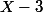 ; il vient
; il vient
=X^3-13X+12=(X-3)(X^2+3X-4))
Le reste , égal à P(3),est nul.
Exercice 3 question 2
Calcul de=\dfrac{P(X)}{X+4})
en X=-4, il vient le tableau

Le reste de la division de P par est nul. P est divisible par
est nul. P est divisible par ; il vient
; il vient
=X^3-13X+12=(X+4)(X^2-4X+3))
Le reste , égal à P(-4),est nul.
Pour la division de P par X+4:
on a P(-4)=0. On dit alors que -4 est racine du polynôme P. Une racine d'un polynôme est un nombre
réel ou complexe , qui annule le polynôme.
Comme la division euclidienne du polynôme P par (X-(-4))=X+4 donne:
P(X)=(X+4)Q(X)+P(-4)
on voit qu'il est équivalent de dire "P est divisible par X+4" ou P(-4)=0
On doit calculer P'(1) avec la méthode de Horner, donc sans dériver le polynôme. La méthode indiquée par Wiki est assez longue et un peu difficile, je la reporte en fin de notre conversation.
Exercice 3 question 1 (suite)
Calcul de
en X=1, il vient le tableau
Le reste de la division de P par
tu as une erreur sur le polynôme
Le reste de la division , égal à P(1),est nul.
Ta notation
Il faut écrire:
et
Exercice 3 question 2
Calcul de
en X=3, il vient le tableau
Le reste de la division de P par
Le reste , égal à P(3),est nul.
Exercice 3 question 2
Calcul de
en X=-4, il vient le tableau
Le reste de la division de P par
Le reste , égal à P(-4),est nul.
Pour la division de P par X+4:
on a P(-4)=0. On dit alors que -4 est racine du polynôme P. Une racine d'un polynôme est un nombre
réel ou complexe , qui annule le polynôme.
Comme la division euclidienne du polynôme P par (X-(-4))=X+4 donne:
P(X)=(X+4)Q(X)+P(-4)
on voit qu'il est équivalent de dire "P est divisible par X+4" ou P(-4)=0
Re: Exercices sur la méthode de Horner.
Ca y est j'ai enfin compris tout ce que tu m'as dit @mathelot sur la division par (x+4) parce qu'en fait le alpha est de -4 ! Et en effet j'ai corrigé mes erreurs de notation.
J'ai fait un exercice sur la méthode de Lagrange, est-ce que tu peux regarder ? Pour la dernière question,
je ne sais pas comment faire.
http://www.noelshack.com/2022-09-4-1646 ... 200352.jpg
http://www.noelshack.com/2022-09-4-1646 ... n-ex-4.png
Egalement pour l'exercice sept je ne savais pas trop comment démarrer : est-ce qu'il faut faire une division par (x-2) comme dans les précédents exercices ?
http://www.noelshack.com/2022-09-4-1646 ... n-ex-7.png
J'ai fait un exercice sur la méthode de Lagrange, est-ce que tu peux regarder ? Pour la dernière question,
je ne sais pas comment faire.
http://www.noelshack.com/2022-09-4-1646 ... 200352.jpg
http://www.noelshack.com/2022-09-4-1646 ... n-ex-4.png
Egalement pour l'exercice sept je ne savais pas trop comment démarrer : est-ce qu'il faut faire une division par (x-2) comme dans les précédents exercices ?
http://www.noelshack.com/2022-09-4-1646 ... n-ex-7.png
Re: Exercices sur la méthode de Horner.
Exercice 4
l3=-1/4 est erroné.
Base de Lagrange:
=\dfrac{-1}{12}X(X-2)(X-3)=(-1/12)X^3+(5/12)X^2-(1/2)X)
=\dfrac{(X+1)(X-2)(X-3)}{6}=(1/6)X^3-(2/3)X^2+(1/6)X+1)
=\dfrac{(X+1)(X)(X-3)}{-6}=(-1/6)X^3+(1/3)X^2+(1/2)X)
=\dfrac{(X+1)(X)(X-2)}{12}=(1/12)X^3-(1/12)X^2-(1/6)X)
tout calcul fait, on obtient:
=X^2-3X+7)
or=5)
conjecture: La courbe représentative de L est symétrique par rapport à la droite verticale d'équation X=3/2
Exercice 6
=X^3-6X^2+11X-6)
en X=2, il vient le tableau

on en déduit que=0)
P est divisible par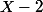
l3=-1/4 est erroné.
Base de Lagrange:
tout calcul fait, on obtient:
or
conjecture: La courbe représentative de L est symétrique par rapport à la droite verticale d'équation X=3/2
Exercice 6
en X=2, il vient le tableau
on en déduit que
P est divisible par
Re: Exercices sur la méthode de Horner.
Il reste un point épineux, c'est le calcul du polynôme dérivé en un point  par la méthode de Horner sans dériver le polynôme !! c'est expliqué dans l'article de Wikipédia .
par la méthode de Horner sans dériver le polynôme !! c'est expliqué dans l'article de Wikipédia .
Re: Exercices sur la méthode de Horner.
Exercice VI
=X3-6X^2+11X-6)
Calcul de P'(2) par la méthode d'Horner
en X=2, il vient le tableau

La 2ème ligne du tableau comprenant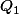 donne
donne
=(X-2)Q_1(X))
En faisant le changement d'indéterminée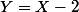 , il vient
, il vient
=Y Q_1(X))
On réitère l'algorithme avec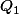 à la place de P:
à la place de P:
la 3ème ligne du tableau avec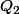 donne:
donne:
=(X-2)Q_2(X)-1)
soit
=Y(YQ_2(X)-1))
la 4ème ligne du tableau avec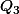 donne:
donne:
=Y)
soit
on définit le polynôme H par:
=P(X+Y))
=H(Y)=Y^3-Y)
or , on a le développement de Taylor de H:
=H(0)+Y H'(0)+\dfrac{Y^2}{2}H''(0)+\dfrac{Y^3}{6}H^{(3)}(0))
d'où
=H'(0)=-1)
Calcul de P'(2) par la méthode d'Horner
en X=2, il vient le tableau
La 2ème ligne du tableau comprenant
En faisant le changement d'indéterminée
On réitère l'algorithme avec
la 3ème ligne du tableau avec
soit
la 4ème ligne du tableau avec
soit
on définit le polynôme H par:
or , on a le développement de Taylor de H:
d'où
Re: Exercices sur la méthode de Horner.
Coucou @mathelot en effet après correction je trouve que L3 est égal à -1/6 et que la somme des coeff est égale à 4 sur 3 au final.
Pour l'exercice j'ai enfin compris la méthode d'Horner merci j'ai fait tout comme toi et ai eu juste.
PS : Tu sais que tu me corriges mieux que mon prof ? Je lui ai envoyé l'exo deux et trois et il m'a dit qu'A PRIORI tout était bon alors qu'il y avait plein d'erreurs (les boules)
Pour l'exercice j'ai enfin compris la méthode d'Horner merci j'ai fait tout comme toi et ai eu juste.
PS : Tu sais que tu me corriges mieux que mon prof ? Je lui ai envoyé l'exo deux et trois et il m'a dit qu'A PRIORI tout était bon alors qu'il y avait plein d'erreurs (les boules)
Re: Exercices sur la méthode de Horner.
Je me suis demandé,as tu eu le temps de lire les trois paragraphes de l'article de wiki sur la méthode de Horner ? Sinon c'est plutôt des bonnes nouvelles que tu m'écris
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
