Salut a tous!
Mon premier message sur ce forum, j'ai cet exercice a faire mais je ne comprend vraiment rien, merci par avance de votre aide!
(il s'agit ici d'un devoirs sur les vecteurs et les matrices)
Trouvez la distance la plus courte entre les points de ces lignes droites :
X + Y - Z = 1,
2X + Z = 3,
X = Y = Z - 1
Exercice de Math Vecteurs et Equations
12 messages
- Page 1 sur 1
Re: Exercice de Math Vecteurs et Equations
L'énoncé est un peu brut.
Essaie de reformuler l'énoncé... Pour que ce soit bien clair, il faut 8 ou 10 lignes . Pas 4 lignes comme ici.
Vas-y. Réécris les informations dont on dispose. Puis dans un second temps, réécris la question.
La première étape, c'est de bien comprendre de quoi on parle. Ensuite, il faudra trouver quels calculs on doit faire, mais ça vient après.
Essaie de reformuler l'énoncé... Pour que ce soit bien clair, il faut 8 ou 10 lignes . Pas 4 lignes comme ici.
Vas-y. Réécris les informations dont on dispose. Puis dans un second temps, réécris la question.
La première étape, c'est de bien comprendre de quoi on parle. Ensuite, il faudra trouver quels calculs on doit faire, mais ça vient après.
Re: Exercice de Math Vecteurs et Equations
Désolé pour cela, donc, pour résumer, je suis étudiant dans une université Russe, et mon sujet est donc en
russe.
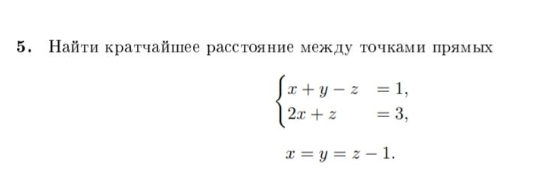
Cet exercice est indépendant du reste de la page, il n'est relié a rien.
La suite des exercices sont liés a la recherche d'aires de triangles de vecteurs et sur les calculs des coordonnées de vecteurs.
La traduction de l'exercice est : Trouvez la distance la plus courte entre les points des droites :
En anglais je sais que cela est : The shortest distance between skew lines mais en Français je ne sais pas du tout.
russe.
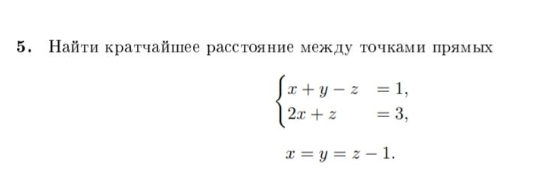
Cet exercice est indépendant du reste de la page, il n'est relié a rien.
La suite des exercices sont liés a la recherche d'aires de triangles de vecteurs et sur les calculs des coordonnées de vecteurs.
La traduction de l'exercice est : Trouvez la distance la plus courte entre les points des droites :
En anglais je sais que cela est : The shortest distance between skew lines mais en Français je ne sais pas du tout.
Modifié en dernier par Azerto le 20 Oct 2021, 21:18, modifié 1 fois.
Re: Exercice de Math Vecteurs et Equations
Oui, moi, j'avais compris.
Ce que je te proposais, c'est de réécrire l'énoncé avec tes mots :
On a une droite ...
On a une autre droite...
On cherche ...
Et il faut remplacer chaque ... par 1 ou 2 lignes d'explication.
Ce que je te proposais, c'est de réécrire l'énoncé avec tes mots :
On a une droite ...
On a une autre droite...
On cherche ...
Et il faut remplacer chaque ... par 1 ou 2 lignes d'explication.
Re: Exercice de Math Vecteurs et Equations
Je dirais alors;
on a un système de 2 équations a 3 inconnues (voir l'image) il y a donc une infinité de possibilités (si je ne me trompe pas)
On doit trouver la plus petite distance possible entre deux vecteurs de coordonnées x y et z tirés de ce système.
Si j'ai bien compris bien sur.
on a un système de 2 équations a 3 inconnues (voir l'image) il y a donc une infinité de possibilités (si je ne me trompe pas)
On doit trouver la plus petite distance possible entre deux vecteurs de coordonnées x y et z tirés de ce système.
Si j'ai bien compris bien sur.
Re: Exercice de Math Vecteurs et Equations
Bonjour,
voici les étapes que j'ai suivies:
1) j'ai écrit les équations des deux droites (D) et (D') sous forme paramétrique:
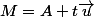
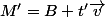
où M et A sont des points de (D) et B,M' des points de (D')
2) en suite, j'ai calculé le carré de la distance de M à M', en fonction de t et t'
on trouve que ce carré^2) est un polynôme de degré 2 des variables t et t'.
est un polynôme de degré 2 des variables t et t'.
3) Pour chercher le minimum de cette distance, j'ai calculé ses dérivées partielles
par rapport à t et t'.
4) Puis j'ai annulé les dérivées partielles (recherche du minimum)
ce qui m'a donné un système linéaire d'inconnues t et t' , à deux inconnues et deux équations.
5) En résolvant le système, ça donne deux points,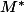 sur (D) et
sur (D) et 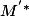 sur (D')
sur (D')
vérifiant :
pour tout M de (D) , pour tout M' de (D') :
^2 \leq d(M;M^{'})^2)
NB: pour vérifier les (longs) calculs, on doit avoir que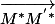 est orthogonal à
est orthogonal à  et
et 
voici les étapes que j'ai suivies:
1) j'ai écrit les équations des deux droites (D) et (D') sous forme paramétrique:
où M et A sont des points de (D) et B,M' des points de (D')
2) en suite, j'ai calculé le carré de la distance de M à M', en fonction de t et t'
on trouve que ce carré
3) Pour chercher le minimum de cette distance, j'ai calculé ses dérivées partielles
par rapport à t et t'.
4) Puis j'ai annulé les dérivées partielles (recherche du minimum)
ce qui m'a donné un système linéaire d'inconnues t et t' , à deux inconnues et deux équations.
5) En résolvant le système, ça donne deux points,
vérifiant :
pour tout M de (D) , pour tout M' de (D') :
NB: pour vérifier les (longs) calculs, on doit avoir que
Modifié en dernier par mathelot le 21 Oct 2021, 18:44, modifié 1 fois.
Re: Exercice de Math Vecteurs et Equations
question (2)
calcul du carré de la distance de M à M':
^2=(5/2-(1/2)t-t')^2+(1/2+(3/2)t-t')^2+(t-t')^2)
calcul du carré de la distance de M à M':
Modifié en dernier par mathelot le 21 Oct 2021, 18:38, modifié 1 fois.
Re: Exercice de Math Vecteurs et Equations
questions (3) et (4):
On dérive^2) par rapport à t, puis par rapport à t', et on égalise les dérivées à 0:
par rapport à t, puis par rapport à t', et on égalise les dérivées à 0:
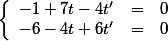
On dérive
Re: Exercice de Math Vecteurs et Equations
question (5):
on résout le système:
t=15/13 et t'=23/13
On a donc comme solutions:
pour (D)
)
pour (D')
)
la distance entre les droites vaut: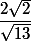
vérification des calculs:
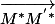 est orthogonal à
est orthogonal à  et
et 
on résout le système:
t=15/13 et t'=23/13
On a donc comme solutions:
pour (D)
pour (D')
la distance entre les droites vaut:
vérification des calculs:
Re: Exercice de Math Vecteurs et Equations
Azerto a écrit:Désolé pour cela, donc, pour résumer, je suis étudiant dans une université Russe, et mon sujet est donc en
russe.
.
décidement, le russe est à la mode sur maths-forum !
Re: Exercice de Math Vecteurs et Equations
Un immense merci a toi pour tes réponses détaillées et précises, je te souhaite une excellente soirée !
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
