bonsoir
c'est moi encore :we:
cette fois ci j'ai un exo de géométrie. si vous pouviez m'aider ça sera tres gentille.
On considere les deux points P appartenant a (x'x) et Q apartenant à (y'y) tels qu OP+OQ=a a reel fixé. (OP et OQ sont des mesures algébriques)
on construit ensuite le carré PRQS de diagonale PQ.
Montere que l'un des points R ou S reste fixe et trouver l'ensemble des positions de l'autre lorsque P varie sur (x'x).
merci d'avance :++:
Exercice de géométrie
5 messages
- Page 1 sur 1
Bonjour,
il est surprenant que l'exercice soit donné à brûle pourpoint.
Enfin....
Considère le triangle rectangle isocèle OAB A(a ; 0) et B(0 ; a)
Appelle I le milieu de [AB]
Considère la rotation de centre I et d'angle - pi/2 et montre que r(P) = Q, donc RIQ est isocèle rectangle en I
ceci te permet de prouver que, dans le carré PRQS, R ou S est confondu avec I (je choisis de dire que R = I)
Considère ensuite le milieu J de [PQ] et montre que J parcourt une droite (d)parallèle à (AB) et passant par le milieu de [IO]
Ensuite utilise l'homothétie de centre I et de rapport 2 qui transforme J en S
Quel est le lieu de S quand J parcourt (d) ?
il est surprenant que l'exercice soit donné à brûle pourpoint.
Enfin....
Considère le triangle rectangle isocèle OAB A(a ; 0) et B(0 ; a)
Appelle I le milieu de [AB]
Considère la rotation de centre I et d'angle - pi/2 et montre que r(P) = Q, donc RIQ est isocèle rectangle en I
ceci te permet de prouver que, dans le carré PRQS, R ou S est confondu avec I (je choisis de dire que R = I)
Considère ensuite le milieu J de [PQ] et montre que J parcourt une droite (d)parallèle à (AB) et passant par le milieu de [IO]
Ensuite utilise l'homothétie de centre I et de rapport 2 qui transforme J en S
Quel est le lieu de S quand J parcourt (d) ?
Je vais faire ça bestialement (car je sais être bestial quand ça m'arrange) avec des coordonnées (en fait des complexes).
J'identifie les points et leurs affixes pour gagner du temps
P vaut donc x, et Q i(a-x). Le milieu de [PQ] est I d'affixe}2)
Les points R et S sont les images respectivement de P et de Q par la rotation de centre I et d'angle
On a donc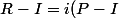) soit
soit 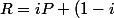I=iP+(1-i)\frac{P+Q}2) et
et
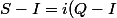) soit
soit 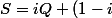\frac{P+Q}2)
Je te laisse finir
J'identifie les points et leurs affixes pour gagner du temps
P vaut donc x, et Q i(a-x). Le milieu de [PQ] est I d'affixe
Les points R et S sont les images respectivement de P et de Q par la rotation de centre I et d'angle
On a donc
Je te laisse finir
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
