bonjour, j'ai un petit exo concernant la nature d'une serie. il faut utiliser les developpements limités mais je me perd a la fin avec tous les restes et tout.
voici l'énoncé :
soit an= (-1+ ch(1/n)) ^(th(1/n))
montrer que lim an = 1 quand n tend vers l'infini ( j'y arrive en faisant des DL a l'ordre 2 de ch th et ln(1+x)
etudier la nature de la serie de terme general un=1-an
(la je bloque, j'ai essayé les DL mais je pense que ca me mène a quelque chose de faux)
merci d'avance pour votre aide
Etude d'une serie (fonction hyperbolique)
6 messages
- Page 1 sur 1
par fabulous » 29 Déc 2008, 12:11
j'arrive a des produit d'exponentielle : exp(-ln(2n²)/n)exp(-ln(2n²)/n*eps1(n))exp(eps2(n)/n)exp(eps3(n)*eps4(n)/n²)
mais si je fais le DL de exp de chaque composante je suis bloquée
mais si je fais le DL de exp de chaque composante je suis bloquée
par XENSECP » 29 Déc 2008, 19:05
Effectivement par DL tu dois pouvoir montrer sa convergence !
Alors:
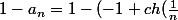) ^{th(\frac{1}{n})})
Or ~ x en 0)
En effet, = \frac{sh(x)}{ch(x)})
 = 1 et sh(x) = \frac{e^{x}-e^{-x}}{2} = \frac{(1 + x + o(x^2)) - (1 - x + o(x^2))}{2} = x + o(x^2))
Donc quand n -> oo 1/n -> 0 donc = \frac{1}{n} + o(\frac{1}{n^2}))
On obtient donc :
)})
)})
Alors:
Or
En effet,
Donc quand n -> oo 1/n -> 0 donc
On obtient donc :
par fabulous » 29 Déc 2008, 22:43
on a le droit de composer des equivalences? car la ce ne sont pas des DL vu qu'il manque les o(1/n²) dans les dernieres expressions?!
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :