Bonjour, j'ai un exercice de maths assez banale :
u0 appartient a ]1,2[ et pour tout n appartenant à N , un+1=racine(3un-2)
Etudier la convergence de la suite (un).
Le problème est que j'ai toujours étudier des convergences avec u0 fixé, je ne sais donc pas comment m' y prendre pour commencer.
J'aimerais utiliser le principe de récurrence pour encadré un, puis de chercher si il y a ne relation entre un et un+1. Trouver une suite géométrique et étudier cette dernière.
Je ne sais pas si c'est le bon chemin à prendre mais mon premier problème est de débuté avec un u0 qui est un intervalle..
Merci pour votre aide
Etude d'une convergence d'une suite
13 messages
- Page 1 sur 1
Hello,
As-tu tracé la courbe y = sqrt(3x-2) ?
As-tu tracé les droites x = 1 et x = 2 ?
u0 -- contrairement à ce que tu penses -- est fixé. Il est fixé entre 1 et 2...
Essaies d'en prendre un au hasard et de tracer quelques termes avec la méthode de l'escalier.
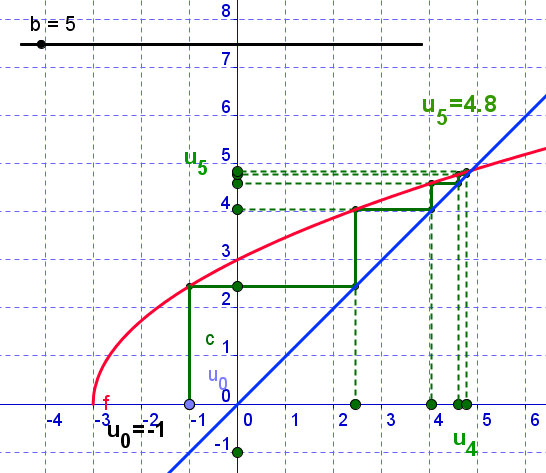
(Cette image ne représente pas ta situation. C'est un exemple)
As-tu tracé la courbe y = sqrt(3x-2) ?
As-tu tracé les droites x = 1 et x = 2 ?
u0 -- contrairement à ce que tu penses -- est fixé. Il est fixé entre 1 et 2...
Essaies d'en prendre un au hasard et de tracer quelques termes avec la méthode de l'escalier.

(Cette image ne représente pas ta situation. C'est un exemple)
Bonjour
La relation tu l'as déjà, elle t'est donnée,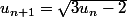 .
.
 est dans un intervalle et non
est dans un intervalle et non  est un intervalle.
est un intervalle.
Dans ce type d'exercice) , on essaie de montrer que la suite est monotone bornée en utilisant les propriétés de la fonction f et ceci fait on détermine sa limite.
, on essaie de montrer que la suite est monotone bornée en utilisant les propriétés de la fonction f et ceci fait on détermine sa limite.
u_0 est donné soit sous forme de valeur numérique soit sous forme d'un paramètre (c'est le cas ici)
Si tu es perdu avec le paramètre, tu peut prendre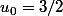 pour voir et revenir ensuite au cas
pour voir et revenir ensuite au cas 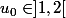
Maxdu21Eiffel a écrit:J'aimerais utiliser le principe de récurrence pour encadré un, puis de chercher si il y a ne relation entre un et un+1. Trouver une suite géométrique et étudier cette dernière.
Je ne sais pas si c'est le bon chemin à prendre mais mon premier problème est de débuté avec un u0 qui est un intervalle..
La relation tu l'as déjà, elle t'est donnée,
Dans ce type d'exercice
u_0 est donné soit sous forme de valeur numérique soit sous forme d'un paramètre (c'est le cas ici)
Si tu es perdu avec le paramètre, tu peut prendre
D'abord j'ai pensé à étudier la monotonie de la suite  .
.
Comme c'est une suite à termes positifs, comparer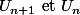 revient à comparer leurs carrés. On se retrouve avec une équation du second degré dont les racines sont 1 et 2. En ètudiant le signes, on établit facilement que si Un est dans ]1,2[ alors Un+1>Un et on peut démontrer par récurrence que
revient à comparer leurs carrés. On se retrouve avec une équation du second degré dont les racines sont 1 et 2. En ètudiant le signes, on établit facilement que si Un est dans ]1,2[ alors Un+1>Un et on peut démontrer par récurrence que 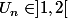 quel que soit n.
quel que soit n.
En somme, est une suite bornée et croissante, donc elle converge. Vers quoi?? ça je l'ignore!
est une suite bornée et croissante, donc elle converge. Vers quoi?? ça je l'ignore!
Comme c'est une suite à termes positifs, comparer
En somme,
Bonsoir.
Des fois, il est plus simple pour étudier la monotonie de (U_n) d'étudier le signe de=x-f (x)) sur un un intervalle borné I contenant
sur un un intervalle borné I contenant  (il est ici donné). De plus, si à partir du tableau de variation
(il est ici donné). De plus, si à partir du tableau de variation  , on montre que si
, on montre que si  \subset I) , la suite sera bien bornée.
, la suite sera bien bornée.
On utilise cette méthode si on a des difficultés pour la comparaison directe de et
et  .
.
PS:
Cette méthode est traité en général dans le cours sur les suites numériques.
soradia1 a écrit:D'abord j'ai pensé à étudier la monotonie de la suite.
Comme c'est une suite à termes positifs, comparer!
Des fois, il est plus simple pour étudier la monotonie de (U_n) d'étudier le signe de
On utilise cette méthode si on a des difficultés pour la comparaison directe de
PS:
Cette méthode est traité en général dans le cours sur les suites numériques.
deltab a écrit:Bonsoir.
Des fois, il est plus simple pour étudier la monotonie de (U_n) d'étudier le signe desur un un intervalle borné I contenant
(il est ici donné). De plus, si à partir du tableau de variation
, on montre que si
, la suite sera bien bornée.
On utilise cette méthode si on a des difficultés pour la comparaison directe deet
.
PS:
Cette méthode est traité en général dans le cours sur les suites numériques.
Merci beaucoup!
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

