étude de signe d'une suite

[thom12]

Bonjour,

je bloque sur un exercice avec mes copains. l'énoncé est le suivant :
on a la suite :
u_o=10
u_(n+1)=(1/2)u_n + 3

nous avons montré que u_(n+1) - u_n = (1/2)( u_n - u_(n-1) ) (équation 1)

il faut ensuite déduire de l'équation 1 que u_(n+1) - u_n a le même signe que u_1 - u_0.

Je vous remercie d'avance pour vos réponses;

[Vassillia]

Bonjour,

Il est possible d’exprimer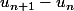 en fonction de 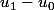à partir de l'équation 1 ce qui peut donner la réponse directement ou alors de raisonner par récurrence sur le signe de et le signe de 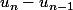(mais cela me parait moins optimisé pour la suite probable de l'exercice).

[thom12]

Bonjour,

je vous remercie pour votre aide. je vais essayer et vous tiens au courant.

[thom12]

Bonjour,

je reviens vers vous car je bloque toujours. je n'arrive pas à montrer par récurrence que u_(n+1) < u_n. Merci de votre aide.

[hdci]

Bonjour,

Comment avez-vous tenté la récurrence ? Indiquez ici précisément ce que vous avez fait pour qu'on puisse vous corriger.

Remarque : la récurrence n'est pas forcément le meilleur moyen ici ; mais comme le raisonnement par récurrence est un incontournable à bien maîtrisé, autant que l'on corrige vos difficultés dans ce cas (on vous indiquera l'autre moyen après)

[lyceen95]

Dans un exercice comme ça, souvent, on a besoin d'utiliser le résultat de la question 1 pour la question 2, et ainsi de suite.
D'ailleurs, l'énoncé donne un gros indice : il dit 'En déduire'.

En déduire , dans un exercice, ça veut dire que la nouvelle question est plus simple que la précédente.
Dans la question 1, tu as fait les 3/4 du chemin, il faut juste finir un certain raisonnement pour arriver au résultat.

Une question qui commence par 'en déduire' est toujours une question simple.

Par ailleurs, on te demande de montrer que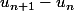 est de même signe que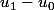
et toi, tu as reformulé ça en 'je dois montrer que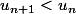 . Ok, c'est exact. Mais tu t'éloignes de la solution. Tu as fait un pas en arrière, et non un pas en avant.

[thom12]

Bonjour,

Comment avez-vous tenté la récurrence ? Indiquez ici précisément ce que vous avez fait pour qu'on puisse vous corriger.

Remarque : la récurrence n'est pas forcément le meilleur moyen ici ; mais comme le raisonnement par récurrence est un incontournable à bien maîtrisé, autant que l'on corrige vos difficultés dans ce cas (on vous indiquera l'autre moyen après)

Merci pour votre réponse. pour la récurrence :
j'ai écrit : u_(n+1) < u_n,
puis multiplié chaque membre par (1/2)
ensuite j'ai ajouté 3 à chaque membre, ce qui m'a permis de retrouver u_(n+1) à gauche. J'ai par la suite remplacé u_(n+1) par son expression par rapport à u_n.
Je me doute bien que quelque chose ne va pas.

merci

[thom12]

Dans un exercice comme ça, souvent, on a besoin d'utiliser le résultat de la question 1 pour la question 2, et ainsi de suite.
D'ailleurs, l'énoncé donne un gros indice : il dit 'En déduire'.

En déduire , dans un exercice, ça veut dire que la nouvelle question est plus simple que la précédente.
Dans la question 1, tu as fait les 3/4 du chemin, il faut juste finir un certain raisonnement pour arriver au résultat.

Une question qui commence par 'en déduire' est toujours une question simple.

Par ailleurs, on te demande de montrer que est de même signe que
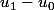
et toi, tu as reformulé ça en 'je dois montrer que . Ok, c'est exact. Mais tu t'éloignes de la solution. Tu as fait un pas en arrière, et non un pas en avant.

Bonjour,

Merci pour votre aide. j'ai pensé écrire u_2 - u_1 = (1/2)(u_1 - u_0), comme cela est négatif, je conclus que c'est effectivement du même signe que (u_1 - u_0). Je trouve cela tout de même trop simple. je me trompe ? merci

[hdci]

Merci pour votre réponse. pour la récurrence :
j'ai écrit : u_(n+1) < u_n,
puis multiplié chaque membre par (1/2)
ensuite j'ai ajouté 3 à chaque membre, ce qui m'a permis de retrouver u_(n+1) à gauche. J'ai par la suite remplacé u_(n+1) par son expression par rapport à u_n.
Je me doute bien que quelque chose ne va pas.

Effectivement, ça ne va pas. Vous voulez montrer par récurrence que pour tout , le signe de est le même que le signe de

Donc la propriété à démontrer est "pour tout , le signe de est le même que le signe de "

Une récurrence commence TOUJOURS par l'initialisation : il faut vérifier que c'est vrai pour le premier indice n, donc ici pour n=0.

Donc, est-ce que le signe de est le même que le signe de ? (la question peut sembler "évidente", mais il faut quand même l'indiquer c'est obligatoire car la récurrence ne marche que si le point de départ est vrai ; pensez aux dominos qui s'enchaînent : si vous ne faites pas tomber le premier domino, vous ne pouvez pas être certain que les autres vont tomber...)

Ensuite, on fait l'hérédité : on suppose que c'est vrai au rang n, et on démontre qu'alors c'est vrai au rang n+1.

Donc on suppose que est du même signe que (rang n), et on veut montrer que est du même signe que (rang n+1 : j'ai remplacé partout n par n+1).

Or vous avez déjà obtenu que pour tout n,
Donc en particulieren remplaçant dans cette dernière formule n par n+1 (puisque cette égalité est vraie pour tous les entiers naturels), cela donne

Essayez de poursuivre

Remarque : ici, je ne cherche même pas à savoir si est négatif ou positif, donc je ne cherche pas à calcule . On pourrait le faire et comme , on a alors et il suffirait de remplacer dans le raisonnement par récurrence "même signe" par "négatif", mais cela ne change absolument rien au principe.

[thom12]

Merci pour votre réponse. pour la récurrence :
j'ai écrit : u_(n+1) < u_n,
puis multiplié chaque membre par (1/2)
ensuite j'ai ajouté 3 à chaque membre, ce qui m'a permis de retrouver u_(n+1) à gauche. J'ai par la suite remplacé u_(n+1) par son expression par rapport à u_n.
Je me doute bien que quelque chose ne va pas.

Effectivement, ça ne va pas. Vous voulez montrer par récurrence que pour tout , le signe de est le même que le signe de

Donc la propriété à démontrer est "pour tout , le signe de est le même que le signe de "

Une récurrence commence TOUJOURS par l'initialisation : il faut vérifier que c'est vrai pour le premier indice n, donc ici pour n=0.

Donc, est-ce que le signe de est le même que le signe de ? (la question peut sembler "évidente", mais il faut quand même l'indiquer c'est obligatoire car la récurrence ne marche que si le point de départ est vrai ; pensez aux dominos qui s'enchaînent : si vous ne faites pas tomber le premier domino, vous ne pouvez pas être certain que les autres vont tomber...)

Ensuite, on fait l'hérédité : on suppose que c'est vrai au rang n, et on démontre qu'alors c'est vrai au rang n+1.

Donc on suppose que est du même signe que (rang n), et on veut montrer que est du même signe que (rang n+1 : j'ai remplacé partout n par n+1).

Or vous avez déjà obtenu que pour tout n,
Donc en particulieren remplaçant dans cette dernière formule n par n+1 (puisque cette égalité est vraie pour tous les entiers naturels), cela donne

Essayez de poursuivre

Remarque : ici, je ne cherche même pas à savoir si est négatif ou positif, donc je ne cherche pas à calcule . On pourrait le faire et comme , on a alors et il suffirait de remplacer dans le raisonnement par récurrence "même signe" par "négatif", mais cela ne change absolument rien au principe.

merci pour ces explications.
si je continue, je trouve au rang n+1 que u_(n+2) - u_(n+1) = (1/2) (u_(n+1) - u_n). est ce que nous pouvons prouver cette hérédité en disant que u_(n+2) - u_(n+1) a le même signe que u_(n+1) - u_n (à l'étape précédente on supposait vrai que u_(n+1) - u_n a le même signe que u_1 - u_0.
est ce aussi possible (sans passer par la récurrence) d'écrire u_2 - u_1 = (1/2)( u_1 - u_0). le signe de u_2 - u_1 est celui de u_1 - u_0 (je ne sais pas si on peut généraliser pour tout n).
merci pour le temps que vous consacrez à mes question

[Vassillia]

je trouve au rang n+1 que u_(n+2) - u_(n+1) = (1/2) (u_(n+1) - u_n). est ce que nous pouvons prouver cette hérédité en disant que u_(n+2) - u_(n+1) a le même signe que u_(n+1) - u_n (à l'étape précédente on supposait vrai que u_(n+1) - u_n a le même signe que u_1 - u_0.

Exact. On peut donc conclure que a le même signe que qui a lui même le même signe que selon notre hypothèse donc la propriété est vraie pour tout n entier positif

Sinon, on pouvait aussi écrire que , tu peux essayer de le montrer à nouveau par récurrence si cela ne te semble pas évident. Cette égalité permet de déduire directement le signe.

[lyceen95]

Toutes ces démonstrations sont des démonstrations par récurrence, plus ou moins bien rédigées.

Donc, faut pas se priver, il y a un mot clair, reconnu, attendu par le prof, c'est le mot "démonstration par récurrence". Tourner autour du pot pour ne pas employer ce mot, ce sera interprété ainsi : "l'élève n'a même pas vu que c'était une démonstration par récurrence".

Je pense qu'une phrase comme celle-ci suffit :
Par récurrence, on en déduit que tous les termes de la forme sont de même signe, et donc du même signe que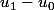
En tout cas, si j'étais prof, ce serait ma réponse 'type' . Plus long, ce serait redondant avec la question précedente, et plus court, ça ne paraît pas facile.

[Vassillia]

Je suis d’accord sur le principe mais à partir du moment où on connait les suites, il n’y a plus vraiment besoin de "démontrer par récurrence" cette égalité. Il suffit d'écrire qu'on reconnait une suite géométrique de raison 1/2 et l'égalité s'obtient directement mais j'admets volontiers qu’on utilise de la récurrence sans le dire.
Comme je ne connais pas le niveau d'étude, je ne me prononce pas sur les exigences de rédaction, il vaut mieux en faire trop que pas assez, c'est certain.

[hdci]

Une fois qu'on a repéré la suite géométrique effectivement pour le niveau "terminale spécialité" c'est suffisant (et même en "1ère spécialité"). On peut alors rédiger en disant "soit la suite définie par..." avec la formule trouvée initialement, puis "on constate que est géométrique de raison 1/2 donc tous ses termes sont du signe de ".

Si on fait la récurrence, comme désormais la récurrence s'apprend en terminale (il y a quelques décennies c'était en seconde...), que c'est nouveau, que les élèves sont très peu habitués aux techniques de raisonnement en général, je demande à mes élèves d'écrire "Initialisation : " (puis la preuve de l'init), "Hérédité : supposons que ce soit vrai au rang n" puis la preuve de l'hérédité, et enfin "Conclusion : l'initialisation et l'hérédité montrent par récurrence que ...".

[lyceen95]

Oui, il manquait un mot ou 2 dans ma proposition.
Dans la question 1, on a montré qu'on avait un facteur 1/2 dans cette nouvelle suite, on a donc tous les éléments pour aller vers une suite géométrique.
On a dit qu'entre 2 termes consécutifs, on avait un facteur 1/2, mais on n'a pas dit qu'entre 2 termes consécutifs, le signe ne changeait pas. Donc il faut le dire.
Ou il faut dire qu'on a une suite géométrique, de raison 1/2 (réel positif), donc tous les membres de cette suite ont le même signe.

[thom12]

Bonjour,

je vous remercie pour vos réponses et toutes ces précisions qui m'aident beaucoup. je précise que l'exercice est de niveau licence 1 (gestion).