Estimation temps sur une course à pied

[poms63]

En course à pied, il existe un paramètre sans unité appelé IE (Indice d'Endurance) représentant la capacité à tenir un effort donné pendant une certaine durée. Pour une course de distance D en km, courue en un temps T en heure, et connaissant sa VMA (Vitesse Maximum Aérobie) en kms/h, on peut calculer son IE grâce à la formule:
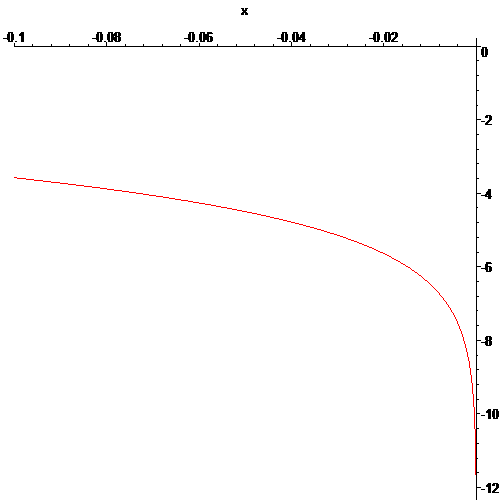
IE = ( (100x(D/T) / VMA ) -100 ) / ln (T / 6)

Exemple pour un semi-marathon:
D = 21,097 kms
T = 1,667 h (soit 100,00 mn ou 1h 40mn )
VMA = 15,00 kms/h
=> alors IE = -5,55

Pour information: -12 (voire -13) pour un coureur débutant, -10 pour un coureur à faible endurance, -7 ou -8 pour un coureur à l'endurance moyenne, -5 pour un coureur très endurant, (-3 voire -2) pour un élite.

Question: A l'inverse, connaissant la distance D d'une course, son indice d'endurance IE, et sa VMA, comment calculer le temps T estimatif pour parcourir la distance ?

Merci d'avance

[leon1789]

Bonjour

D'une part, avec votre formule initiale, je ne trouve pas votre résultat IE = -5.55 , mais IE = 12.20 car
(100*(D/T) / VMA ) -100 = -15.63 et ln (T / 6) = -1.28 environ.
Il y a-t-il une erreur de frappe quelque part ? ou autre chose...

D'autre part, on peut évidemment faire une résolution numérique (par logiciel de calcul dédié, ou un tableur par exemple).

Mais cela peut être intéressant d'avoir une formule donnant approximativement la solution.
Sauf erreur de ma part, la solution est donnée littéralement par cette formule

Le problème est l'utilisation de la fonction LambertW que peu de logiciels connaissent.
On pourrait chercher à approcher numériquement cette fonction.
Pour cela, il faudrait un encadrement relativement petit de

Pouvez-vous donner des infos numériques sur D, VMA, et IE ?

[catamat]

Bonjour

Dans la formule : Indice endurance = (% de VMA maintenu pendant la course – 100) / ln (temps de course en minute / 6)
le temps dans le log est exprimé en minutes, il s'agit donc de 60T si T est en heures.
On trouve bien -5.55

[leon1789]

ok, dans la partie (100x(D/T) / VMA ) -100 , le temps T est en heure,
et dans la partie ln (T / 6) , le temps T est en minutes.
Bon, il faut choisir entre exprimer le temps en heure ou en minutes, mais pas le deux... surtout qu'il faut résoudre une équation en T !
Disons qu'on choisisse que T soit un temps en heure. La formule devient

cohérente avec l'exemple donné :
D = 21,097 kms
T = 1,667 h
VMA = 15,00 kms/h
=> alors IE = -5,55

Et la solution donnant T (en heure) est donc (avec la formule corrigée) :



Je précise, pour ceux qui connaissent la fonction de W de Lambert, que la solution suit la branche secondaire de la fonction. Voir https://fr.wikipedia.org/wiki/Fonction_W_de_Lambert (notée ).


Pour continuer, pouvez-vous donner des infos numériques sur D, VMA, et IE ?
dans le but de simplifier la fonction de Lambert de manière satisfaisante.

IE varie entre -2 (élite) et -13 (débutant)
D (distance de course) entre 0 et 1000 ?
VMA ?

[leon1789]

Une autre manière d'écrire la solution :

[leon1789]

Essayons de voir comment on peut approcher la fonction LambertW par des fonctions plus standards.
D'abord, il faut voir où nous nous situons dans le domaine de définition de la fonction. Reprenons l'exemple :
D = 21,097 kms
VMA = 15,00 kms/h
IE = -5.55

Ainsi 100/IE = -18 et D / VMA = 1.4, et comme exp(-100/ IE) = exp(18) est énorme, on comprend alors que la seconde expression de la solution va être bien plus utile que la première.

Ensuite x = 10 * D/VMA * 100/IE * exp(100/IE) = -3.8 * 10^(-6)
donc nous sommes très prêts de 0 !

Regardons le graphe de la fonction LambertW en 0 :

Il y a donc une asymptote, ce qui complique un peu les choses.

L'approximation classique de la fonction LambertW en 0 est
LambertW(x) ~~ ln(-x) - ln(-\ln(-x)) + ln(-ln(-x)) / ln(-x)

Ainsi, la formule que je propose lorsque 10* D/VMA * 100/IE * exp(100/IE) est proche de 0
est
T ~~ D/ VMA * 100/IE * 1/y
avec
x = 10 * D/VMA * 100/IE * exp(100/IE)
y = ln(-x) - ln(-\ln(-x)) + ln(-ln(-x)) / ln(-x)

Testons sur l'exemple :
D = 21,097 kms
VMA = 15,00 kms/h
IE = -5.55
x = -3.8 * 10^(-6)
y = -15.21
T ~~ 1.665

Parfait !

[leon1789]

Autre façon de rédiger le même calcul :
z = ln(-10 * D/VMA * 100/IE) + 100/IE on vérifiera que z < -3 pour que l'approximation soit correcte.
y = z - ln(-z) + ln(-z)/z
T ~~ D/VMA * 100/IE * 1/y

Testons sur l'exemple :
D = 21,097 kms
VMA = 15,00 kms/h
IE = -5.55
z = -12.48 (on a bien z < -3, l'approximation sera correcte)
y = -15.21
on obtient T ~~ 1.666

[leon1789]

J'avoue que j'ai un peu de mal à comprendre que l'on puisse obtenir des résultats avec 4 chiffres significatifs, alors que les données n'en comportent que 2 ou 3. Mais il faudrait que je fasse le calcul moi-même pour le comprendre.

Ceux qui suivent mes recherches et quelque fois mes résultats n'auront aucun mal à résoudre ce problème.

Les données sont bien précisés avec 4 chiffres significatifs.

Avec des telles affirmations, on attend de voir comment résoudre le problème.

[leon1789]

On obtient une fonction de forme R = k . x^a . y^b . z^c
(....)
Il est clair qu'avec des valeurs numériques vraisemblables, une application aiderait à comprendre la méthode.

aucun mal à résoudre ce problème, tu disais ! MDR

Encore une fois, voici ton incapacité à répondre à la question, et même n'avoir aucune intuition sur le résultat. Quand on se vante comme toi, cela totalement ridicule. Simplement cuistre dira-t-on.

[leon1789]

Autre façon de rédiger le même calcul :
z = ln(-10 * D/VMA * 100/IE) + 100/IE on vérifiera que z < -3 pour que l'approximation soit correcte.
y = z - ln(-z) + ln(-z)/z
T ~~ D/VMA * 100/IE * 1/y

Testons sur l'exemple :
D = 21,097 kms
VMA = 15,00 kms/h
IE = -5.55
z = -12.48 (on a bien z < -3, l'approximation sera correcte)
y = -15.21
on obtient T ~~ 1.666

Est-ce que poms63 trouve son compte dans ce calcul ?