Est ce que l'integral (1/(x²+1)^n+1) est egale a (l'integral (1/(x²+1))^n+1?,
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 02 Nov 2008, 15:00
par mostdu95 » 02 Nov 2008, 15:00
bonjour
c'est tout ce que je veux savoir sachant que c'est l'integral de 0 a +00
et merci
-
termi111
- Messages: 5
- Enregistré le: 02 Nov 2008, 15:04
-
 par termi111 » 02 Nov 2008, 15:17
par termi111 » 02 Nov 2008, 15:17
non ce n'est pas egal
c'est egal a (x²+1)^-(n+1)
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 01:06
-
 par HanZel » 02 Nov 2008, 15:29
par HanZel » 02 Nov 2008, 15:29
Si tu veux savoir en gros si :
^n) = (\int f(x))^n)
La réponse est non.
Un contre exemple tout bête :
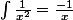
or selon la méthode fausse ça ferait :
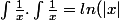.ln(|x|))
J'espere répondre a ta question.
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 02 Nov 2008, 15:39
par mostdu95 » 02 Nov 2008, 15:39
en fait je veux montrer l'existen de l'int( 1/(x²+1)^n+1) de 0 a +00 et donc g fait la dempo de x²+1 et puis je vois que ça converge et tout ......
mais ds ce cas commen justifier l'existance alors par une ipp ptet mais ça me semble pas que c'est la + simple
-
HanZel
- Membre Relatif
- Messages: 106
- Enregistré le: 29 Oct 2008, 01:06
-
 par HanZel » 02 Nov 2008, 15:46
par HanZel » 02 Nov 2008, 15:46
As tu essayé par récurrence? suppose que c'est vrai au rang n et regarde si c'est vrai au rang n+1 avec une ipp
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 02 Nov 2008, 16:01
par mostdu95 » 02 Nov 2008, 16:01
ah oui d'accord donc au rong n+1
et si on a a place de x² ,x^3 on fait aussi une ipp au rong n+1 ?, c'est plus complique je pense on fait comment ds ce cas.....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
