C est dure

[LA solution]

Bonjour tout le monde jai un exo qui me tracasse la tete!!!!! svp aidez moi a le faire
exo:
Soit G un groupe fini distinct de {e} tel que : ;)a ;)G : a2 = e.
1°/ Montrer que G est commutatif.
2°/ Montrer que le cardinal de G est pair (utiliser le théorème de Lagrange).
3°/ Montrer que G est isomorphe à (z/2z)p (et donc |G| = 2p).
jai fait 1) et 2)

[XENSECP]

Salut,

a2 = a^2 tu veux dire ?

[wserdx]

Bonsoir,
j'essaie d'aider "LA solution" par MP. La démonstration que je lui propose passe par le fait que on peut trouver un sous-groupe avec .
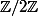Comme est isomorphe à et que 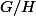vérifie la même propriété que G à savoir que tous ses éléments vérifient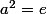
il ne reste plus à vérifier que est isomorphe à , ça démontre alors par récurrence que G est isomorphe à
Quelqu'un peut-il confirmer ce dernier point? Je pense qu'un théorème bien choisi pourrait régler ce problème rapidement. Mes connaissances sur ce sujet sont bien lointaines.

[alm]

Bonjour

il ne reste plus à vérifier que est isomorphe à , ça démontre alors par récurrence que G est isomorphe à

Je crois qu'on n'a pas besoin d'un isomorphisme pour cette avant dernière étape.
On peut juste dénombrer de deux façons différentes et ça suffit largement.
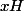Comme les classes d'équivalence modulo sont de la forme avec 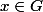ells ont chacune deux éléments et comme elles forment une partition de et que leur nombre est précisément , on a alors
La dernière étape est comme tu l'as dit de raisonner par récurrence sur le cardinale du groupe en tenant compte de tes remarques correctes à mon avis.

[wserdx]

Je pense que l'isomorphisme est indispensable. J'ai essayé de m'en convaincre avec le contre exemple suivant:

ne vérifie pas la propriété a+a = 0 (notation additive au lieu de multiplicative) pour tout a et n'est donc pas isomorphe à

Si on prend qui est bien un sous groupe normal de alors 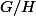a bien aussi deux éléments est donc isomorphe à
et donc dans ce cas n'est pas isomorphe à
J'ai du mal à voir quel est l'argument qui ferait marcher la démonstration...

[wserdx]

Bonsoir,
j'essaie d'aider "LA solution" par MP. La démonstration que je lui propose passe par le fait que on peut trouver un sous-groupe avec .
Comme est isomorphe à et que vérifie la même propriété que G à savoir que tous ses éléments vérifient
il ne reste plus à vérifier que est isomorphe à , ça démontre alors par récurrence que G est isomorphe à
Quelqu'un peut-il confirmer ce dernier point? Je pense qu'un théorème bien choisi pourrait régler ce problème rapidement. Mes connaissances sur ce sujet sont bien lointaines.

J'avais les bons arguments mais pas dans le bon ordre.
En fait, par hypothèse de récurrence, est bien isomorphe à pour un certain , (éventuellement si est réduit à ).
Ensuite, ce n'est pus difficile de montrer que est isomorphe à

[Doraki]

On peut faire la récurrence dans l'autre sens, en utilisant des sous-groupes plutôt que des groupes quotients.

Si on a construit un sous-groupe H isomorphe à Z/2Z^p et que ce sous-groupe n'est pas G,
alors il existe g dans G\H, et on vérifie que le groupe engendré par H et g est isomorphe à (Z/2Z)^(p+1) grâce à la commutativité et le fait que g²=e. Et on répète le procédé jsuqu'à obtenir l'isomorphisme cherché.


Et si on reconnaît qu'on est en train de réécrire le théorème de la base incomplète, on peut faire savant et dire que G est un Z/2Z-espace vectoriel fini, donc de dimension finie, donc isomorphe à Z/2Z^(dim G)