Espérance d'une somme... au carré
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Noisette3
- Messages: 1
- Enregistré le: 13 Jan 2013, 02:39
-
par Noisette3 » 13 Jan 2013, 02:50
Ami(e)s de la nuit, bonsoir.
Après avoir retourné les variables dans tous les sens avec le peu d'énergie qu'il me reste, je n'ai d'autre choix que de quémander une aide externe. En effet, dans l'expression suivante, l'indice de sommation me gêne...
Sachant
=j)
, comment montrer que
^2=j\sum z_t^2)
Merci d'avance
Noisette
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 13 Jan 2013, 12:16
Je suppose que la somme est finie, et que les variables aléatoires en question sont à moyenne nulle et non corrélées. Dans ce cas, on se sert de l'identité
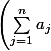^2=\sum_{j=1}^na_j^2+ \sum_{1 \leq i\neq j \leq n}a_ia_j)
et on prend les espérances.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
