Espaces séparables et lp
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par dominique.abgrall » 26 Oct 2008, 12:26
par dominique.abgrall » 26 Oct 2008, 12:26
Bonjour,
est ce quelqu'un aurait une idée pour démontrer que lp pour 1<=p<+infini est séparable et l(+infini) ne l'est pas ?
Merci d'avance
 par legeniedesalpages » 26 Oct 2008, 12:37
par legeniedesalpages » 26 Oct 2008, 12:37
dominique.abgrall a écrit:Bonjour,
est ce quelqu'un aurait une idée pour démontrer que lp pour 1<=p<+infini est séparable et l(+infini) ne l'est pas ?
Merci d'avance
Bonjour,
tu peux montrer que les
)_{i\in \mathbb{N}})
sont denses dans
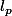
si

, chaque
)
étant la suite qui vaut 1 au

-ième terme, 0 pour les autres termes.
pour montrer que

n'est pas séparable tu peux montrer que les suites à valeurs dans

forment un sous-ensemble infini non dénombrable et que la distance entre deux quelconques de ces suite est 1.
 par dominique.abgrall » 26 Oct 2008, 13:39
par dominique.abgrall » 26 Oct 2008, 13:39
ça me semble pas mal mais comment dire qu'il y a forcément un élément e(i) dans tout voisinage de x de lp ?
 par legeniedesalpages » 26 Oct 2008, 13:54
par legeniedesalpages » 26 Oct 2008, 13:54
non désolé je suis allé trop vite.
Tu montres en fait que
_{i\in \mathbb{N}})
est dense dans
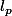
, et que
_{i\in \mathbb{N}})
est dénombrable et dense dans
_{i\in \mathbb{N}})
, par "transitivité" de la densité, il sera aussi dense dans
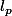
.
_{i\in \mathbb{N}})
étant l'ensemble des combinaisons linéaires à coeff dans

des
_{i\in \mathbb{N}})
.
 par dominique.abgrall » 26 Oct 2008, 14:00
par dominique.abgrall » 26 Oct 2008, 14:00
bon, là ça me semble plus juste.
as tu une référence pour justifier la transitivité de la densité ? Je veux bien mais je ne connaissais pas cette propriété.
Merci
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Oct 2008, 14:11
par Joker62 » 26 Oct 2008, 14:11
Tu veux dire la transitivité de la densité :)
A C B avec A dense dans B
B C C avec B dense dans C
Cela implique-t-il que A est dense dans C ?
Adh(A) = B
Adh(B) = C
=> Adh(B) = Adh(Adh(A)) = Adh(A) = C
 par legeniedesalpages » 26 Oct 2008, 14:21
par legeniedesalpages » 26 Oct 2008, 14:21
dominique.abgrall a écrit:bon, là ça me semble plus juste.
as tu une référence pour justifier la densité de la transitivité ? Je veux bien mais je ne connaissais pas cette propriété.
Merci
euh non, c'est peut être un peu informel comme appelation.
Mais pour tout

, tu peux trouver, quelque soit

,
un
_{i\in \mathbb{N}})
tel que

(par densité de
_{i\in \mathbb{N}})
dans
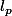
) et tu peux trouver un
_{i\in \mathbb{N}})
tel que

(par densité de
_{i\in \mathbb{N}})
dans
_{i\in \mathbb{N}})
).
ça nous donne

,
ce qui te permet d'établir que
_{i\in \mathbb{N}})
est dense dans
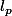
.
 par dominique.abgrall » 26 Oct 2008, 14:54
par dominique.abgrall » 26 Oct 2008, 14:54
effectivement ...
et c'est on ne peut plus simple !
 par dominique.abgrall » 26 Oct 2008, 16:16
par dominique.abgrall » 26 Oct 2008, 16:16
juste un truc ... peux tu me redéfinir les e(j) j dans N pour voir ?
 par legeniedesalpages » 26 Oct 2008, 16:58
par legeniedesalpages » 26 Oct 2008, 16:58
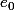
est la suite de réels
)
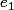
est la suite de réels
)
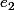
est la suite de réels
)
...
 par dominique.abgrall » 26 Oct 2008, 19:33
par dominique.abgrall » 26 Oct 2008, 19:33
ok, c'est bon
un simple doute m'avait effleuré
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 104 invités
