Espace projectif privé d'hyperplans
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2009, 16:00
par Nightmare » 03 Mar 2009, 16:00
Bonjour :happy3:
Je m'intéresse au problème suivant :
On considère l'espace projectif complexe
)
auquel on retire
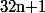
hyperplans
)
où les
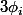
sont des formes linéaires linéairement indépendantes.
Je voudrais démontrer que
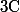
n'est pas holomorphe à cet espace
.
J'arrive à le faire rapidement dans le cas de la sphère de Riemann mais pas la généralisation...
Pour le contexte, je travaille sur les surfaces de Riemann hyperboliques (ie biholomorphes au demi-plan de Poincaré).
Si vous aviez des idées... merci :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2009, 18:03
par Nightmare » 03 Mar 2009, 18:03
Pas d'idées?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Mar 2009, 18:07
par barbu23 » 03 Mar 2009, 18:07
J'aurai aimé t'aider mais sincèrement je ne sais pas ! :hum: :happy2:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2009, 18:14
par Nightmare » 03 Mar 2009, 18:14
Tant pis, merci quand même :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2009, 18:22
par Nightmare » 03 Mar 2009, 18:22
Je ne sais pas si ça aide, mais j'ai prouvé auparavant que
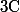
privé de deux points était hyperbolique.
En effet, d'après le théorème de Poincaré, le revêtement universel d'une surface de Riemann est soit biholomorphe à la sphère de Riemann, soit isomorphe au plan complexe, soit biholomorphe au demi-plan de Poincaré.
Or, en vertu de la non compacité et de la non connexité simple du plan complexe privé de deux points, il ne peut être ni biholomorphe à la sphère de Riemann, ni isomorphe au plan complexe donc il est forcément biholomorphe au demi-plan de Poincaré.
J'ai l'impression cependant que ça ne sert à rien pour mon "exercice"...
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
 par R.C. » 03 Mar 2009, 20:39
par R.C. » 03 Mar 2009, 20:39
Bonjour,
J'ai dû mal comprendre le problème, mais quand tu enlève des hypersurfaces à une variété tu obtiens un truc de la même dimension. Donc je vois pas comment C pourrait être biholomorphe à ce que tu obtiens.
Ah en fait je pense que je viens de comprendre : il faut lire C^n. Bon mais là encore, c'est pas très compliqué : si tu enlève un hyperplan tu te retrouve avec C^n, et si tu continue à en enlever, tu change la topologie (connexité par ex...).
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2009, 23:39
par Nightmare » 03 Mar 2009, 23:39
Non c'est bien
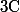
, et on parle d'holomorphisme et pas de biholomorphisme ici.
Ensuite on ne retire pas les hyperplans de façon aléatoire, les formes linéaires sont libres, je pense que c'est important !
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
 par R.C. » 04 Mar 2009, 09:01
par R.C. » 04 Mar 2009, 09:01
J'ai deux questions pour essayer de mieux comprendre le problème :
- Qu'est-ce que ça veut dire ne pas être holomorphe à C ?
- Ces formes linéaires sont elles complexes (je ne pense pas mais bon..) ou réelle (et à ce moment là je ne comprends pas très bien parce que l'hyperplan réel dans C^(n+1) se projette de façon assez horrible sur l'espace projectif) ?
Question subsidiaire : Est-ce que tu peux expliquer comment tu as procédé pour la sphère de Riemann ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Mar 2009, 13:58
par Nightmare » 04 Mar 2009, 13:58
1) Cela veut dire qu'il n'existe pas d'application holomorphe (sauf peut être constante) de
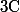
dans notre espace
2) Oui, les formes linéaires sont complexes,
*)
3) Pour la sphère de Riemann c'est un peu long mais j'utilise un théorème Borel sur les unités holomorphes et après je montre que si on prend une application holomorphe du plan dans son compactifié qui évite mes 3 hyperplans alors son image est de dimension nulle.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Mar 2009, 17:01
par Nightmare » 04 Mar 2009, 17:01
C'est bon, problème résolu, j'ai réussi à généraliser. J'étais parti dans la mauvaise direction !
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
 par R.C. » 04 Mar 2009, 17:43
par R.C. » 04 Mar 2009, 17:43
Ahhhh, ne nous laisse pas sur notre faim et dis-nous comment tu t'y prends !!!!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Mar 2009, 18:02
par Nightmare » 04 Mar 2009, 18:02
Comme pour la sphère de Riemann.
Voila en gros les étapes de la démo :
Je note
)
holomorphe et
=\phi_{i}[(f_{0}(z),...,f_{n}(z))])
où les
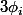
sont mes formes linéaires linéairement indépendante dont les hyperplans en sont les noyaux et les
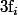
les coordonnées projectives de f.
Je définie aussi (ce n'est pas mon idée) la relation d'équivalence

a) Je montre qu'il y a au plus 1 classe d'équivalence
b) Je considère les applications
,...,\phi_{n}(x)))
et
)
.
Je montre que l'image de la composée
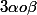
est de dimension au plus 1.
c) En passant au quotient dans l'espace projectif, on a que l'image de f est de dimension nulle.
Utilisateurs parcourant ce forum : catamat et 98 invités
auquel on retire
hyperplans
où les
sont des formes linéaires linéairement indépendantes.
n'est pas holomorphe à cet espace
