Espace normé et suite de cauchy

[muse]

Bonsoir,

Voila l'énoncé:
Soit E un espace vectoriel normé et une suite de Cauchy dans E

1) montrer que pour tout x dans E, la suite de nombres reels ||-x|| a une limite.

Voila les idées que j'ai eu mais bon j'aboutis a rien.
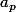
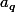
La seul données qu'on ait sont : ||- || 0 quand q,p

Montrer que ||-x|| a une limite revient a montrer que ||-x||L
qui revient a montrer que ||-x-L||0

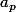
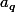
Voila aprse je ne sais pas comment montrer ça a partir de ||- || 0

[ThSQ]

compare | ||a_n-x||-||a_p-x|| | et ||a_n-a_p||

[muse]

Ok donc le premier est plus petit que le deuxieme et donc converge vers 0 ce qui montre que
||a_n-x||-||a_p-x|| --> 0
ce qui veut juste dire que ||a_n-x|| et ||a_p-x|| ont la meme limite mis ça peut trse bien etre l'infinie non ?

[SimonB]

Ta flèche "tend vers" ne signifie rien (tu as deux indices, n et p...).

D'une part, que peux-tu dire de la suite (||a_n-x||) à partir de la propriété que tu viens de démontrer ? D'autre part, dans quel espace prend-elle ses valeurs ?

[muse]

Elle prend ses valeurs dans un espace vectoriel normé E (j'ai mis tous l'énnoncé et la première question)

Alors en effet y'a 2 indices. On a

mais je veux que ça tende vers qqch il faut bien que je fasse tendre n et p vers l'infinie non ?
Je ne sais pas trop quoi dire la

[Doraki]

Elle prend ses valeurs dans un espace vectoriel normé E

Il parlait pas de la suite (an) mais de la suite ( ||an - x|| )

[muse]

Dans R non ?

[Doraki]

Et ça serait pas une suite de Cauchy ?

[muse]

okkkk j'ai compris:


donc

| ||a_q-x||-||a_p-x|| | converge vers 0 donc ||a_n-x|| est de cauchy or la suite ||a_n-x|| est à valeur dans R de plus R est complet
donc au final ||a_n-x|| converge

c'est ça ?

[SimonB]

C'est ça, oui. Sauf que tu as encore dit qu'une expression à deux indices "convergeait vers 0", ce qui n'a pas vraiment de sens précis. Parler de suite de Cauchy directement est plus clair.

[muse]

ha oui j'aurais du dire "converge vers 0 quand p et q tendent vers l'infinie".

Merci beaucoup. Je continue de réfléchir a la suite de l'exercice et je reposterai ici si je n'arrive pas(chose qui va surement arriver :p)

Merci beaucoup

[SimonB]

ha oui j'aurais du dire "converge vers 0 quand p et q tendent vers l'infinie".

Même ceci n'est pas strictement juste. Une phrase qui me semble plus claire serait "quand p et q tendent indépendamment vers l'infini". Mais le plus simple est de parler directement de suite de Cauchy :happy2: