Espace localement compact !

par **barbu23** » 16 Jan 2009, 00:31

Bonjour :
ça fait longtemps que j'ai pas fait de topologie, et j'aimerai que quelqu'un me dit porquoi un espace topologique séparé dans lequel tout point admet un voisinage ouvert homéomorphe à un ouvert de

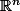
est localement compact.
J'ai un autre truc à vous demander : Est ce que quelqu'un pet m'écrire ici la démonstration du théorème d'invariance du domaine de Brouwer ? Ce sera gentil de sa part, j'ai perdu mon ancien cours qu'on a fait à la fac l'année passé !
Merci d'avance de votre aide !

par **Nightmare** » 16 Jan 2009, 00:43

Salut :happy3:

La compacité locale est invariante par homéomorphisme ! Et dans un espace localement compact, les ouverts sont eux même localement compacts.

par **barbu23** » 16 Jan 2009, 00:49

Ah d'accord Merci Nightmare !

par **Nightmare** » 16 Jan 2009, 00:50

Pour le théorème du domaine d'invariance de Brouwer, je ne savais pas ce que c'était, je viens de voir l'énoncé, ça découle du théorème du point fixe de Brouwer non?

par **ffpower** » 16 Jan 2009, 02:08

Si quelqu un a une demo assez simple du theoreme de l invaraince du domaine,je suis preneur aussi,car c est quand meme un joli énoncé,intuitif et pourtant...Et non ca découle pas du thm de Brouwer(par contre ca découle de Borsuk Ulam)

par **Nightmare** » 16 Jan 2009, 02:30

Effectivement ! :marteau:

Par contre je lisais hier justement un article sur la notion d'homologie et de cohomologie, il me semble qu'on peut trouver une preuve avec ça, m'enfin ce n'est pas élémentaire !

par **Nightmare** » 20 Jan 2009, 13:45

Je remonte le sujet car j'ai enfin réussi à montrer le théorème de manière simple :

Supposons que

et

soient homéomorphes pour

. Ces espaces étant localement compacts, en prolongeant l'homéomorphisme en joignant les points à l'infini, on a que leur compactifiés d'Alexandrov sont aussi homéomorphes.

Or, le compactifié d'Alexandrov de

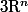
est l'hypersphère

.

Ainsi,

et

sont homéomorphes. Par invariance topologique de la cohomologie de Rham, on aurait

.
Or, on montre rapidement à coup de suites exactes que

(voir

dans le cas p=0) et

. Absurde.

conclusion :

et

ne sont jamais homéomorphes si [tex]3$\rm p\no=q[tex]
:happy3:

par **Nightmare** » 20 Jan 2009, 13:51

Oups, vous aurez corrigé : Le compactifié d'Alexandrov de

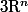
n'est pas l'hypersphère

mais y est homéomorphe.

:happy3:

Espace localement compact !

Espace localement compact !

Qui est en ligne