Espace localement connexe par arc

[Archytas]

Salut,
J'ai un peu de mal avec la notion de "localement connexe par arc" vous avez un exemple simple d'espace connexe par arc et NON localement connexe par arc ?
Et ensuite si vous avez un exemple d'espace semi localement simplement connexe sans être localement simplement connexe.
Merci !

[Robot]

L'exemple classique est celui du peigne dans 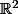dont le manche est le segment horizontal [(0,0), (1,0)] et les dents sont les segments verticaux [(1,n,0),(1/n,1)] pour tout entier n>0 ainsi que le segment [(0,0),(0,1)]. C'est connexe par arcs. On peut aller du point (0,1) au point (1/n,0) dans le voisinage, mais il faut faire un long détour !

[Archytas]

Donc ici il est pas localement connexe à cause de (0,1) ? Il n'existe pas de base de voisinage connexe par arc parce que tout disque rencontrera une dent du peigne c'est ça ?

[Robot]

Oui, pour tout voisinage de (0,1) il existe n tel que le voisinage contienne (1/n,1).

[Archytas]

Et vous avez un exemple d'ensemble non semi localement simplement connexe ? Je vois pas la différence entre avec semi et sans semi

[Robot]

Je ne sais pas ce que veut dire "semi localement simplement connexe".

[Ben314]

"semi localement simplement connexe" = Espace X dans lequel tout point admet un voisinages V tel que tout lacet contenu dans V est homotope dans X (et pas forcément dans V) à un point.

[Ben314]

Et "le" exemple classique d'espace semi localement simplement connexe mais non localement simplement connexe, c'est celui d'un cône C au dessus d'une famille infinie de cercle de rayon 1/n d'un plan tous tangents en un même point O du plan.
Si on prend un petit voisinage V de O, les petits cercles du plan contenus dans ce voisinage seront homotope à un point dans le cône vu que C est trivialement contractile, mais ne seront pas homotope à un point dans V.

[Archytas]

Désolé, je comprends pas bien pourquoi les petits cercles sont homotopes à un point du cône ? Pourquoi la contractibilité du cône l'implique ?

[Ben314]

C'est quoi pour toi la définition d'un espace contractile ?
Et ça te semble pas complètement trivial qu'un cône au dessus d'absolument n'importe quel espace topologique ça va être contractile ?

[Archytas]

Bin le cône oui est contractile. C'est quand son groupe de poincaré est trivial, quand il est simplement connexe, sans poignée quoi, mais si j'ai bien compris c'est comme si on avait attaché des 1-cellule à un point de la base du cône et si on prend un chemin qui enroule un petit cercle dans un voisinage, comment on pourra le contracter en un point ?

[Ben314]

Non, la définition de "être contractile", c'est pas du tout le fait que le groupe fondamental est trivial (je suppose que c'est ça que tu appelle "le groupe de Poincaré" : j'ai la flemme de vérifier). Dire que le groupe fondamental est trivial ça signifie qu'on peut contracter tout les lacets ce qui, (modulo de supposer l'espace connexe par arc) signifie que ton espace est simplement connexe.
Être contractile, ça veut dire que tu peut contracter l'espace tout entier sur un de ces points donc en particulier, tout les autres groupes d'homotopie seront eux aussi triviaux et pas seulement le .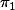
Par exemple, les sphères de dimension >=2 sont simplement connexes, mais pas contractiles.

D'un autre coté, dans le cas présent on s'en fout un peu vu que contractile => simplement connexe et que ça suffit pour dire que tout les lacets du cône sont homotopes à un point.
En plus, visuellement parlant ça me semble complètement trivial : tu fait "remonter" (continument) n'importe quel lacet vers le sommet du cône et clairement, ça le contracte sur le sommet.

[Archytas]

Être contractile, ça veut dire que tu peut contracter l'espace tout entier sur un de ces points donc en particulier, tout les autres groupes d'homotopie seront eux aussi triviaux et pas seulement le .
Par exemple, les sphères de dimension >=2 sont simplement connexes, mais pas contractiles.

Ah ok je savais pas, je pensais qu'il ne s'agissait que du groupe fondamental,merci !

D'un autre coté, dans le cas présent on s'en fout un peu vu que contractile => simplement connexe et que ça suffit pour dire que tout les lacets du cône sont homotopes à un point.
En plus, visuellement parlant ça me semble complètement trivial : tu fait "remonter" (continument) n'importe quel lacet vers le sommet du cône et clairement, ça le contracte sur le sommet.

ça oui je vois mais en dessous il y a plein de cercles qui eux ne sont pas contractiles si ? Pour moi leur groupe de fondamental est le produit libre de Z sur N... Je suis désolé de pas comprendre, je comprends pas ce que l'ajout du cône change . Il est plein ?

[Ben314]

Ben justement, si tu prend juste la famille de cercles dans le plan, c'est pas du tout simplement connexe (donc pas contractile) et ce n'est pas non plus localement simplement connexe vu que dans tout voisinage de O (point de tangence des cercles) tu va trouver des petit cercles qui ne seront pas homotopes a un point, ni en restant dans le voisinage en question, ni même en acceptant d'utiliser l'espace tout entier pour "homotoper" (donc pour le moment, l'espace n'est pas non plus semi localement simplement connexe)

Par contre, le cône C au dessus de la famille de cercle, il est clairement simplement connexe (et même contractile) ce qui implique évidement qu'il est il est semi localement simplement connexe.
Mais, les petits voisinage de O contiennent forcément des petit cercles que tu peut pas contracter en restant dans le petit voisinage (la seule façon de les contracter, c'est de les faire monter au sommet du cône et ça te fait sortir du voisinage) donc l'espace n'est pas localement connexe.

[Archytas]

Ok je pense que je commence à comprendre, mais je vois pas comment tu homotopes les petits cercles en les faisant monter au sommet du cône ? Si on a un élastique qu'on peut pas réduire en un point et qu'on a un cône qu'il touche en O, on lui tire dessus, le fait monter au sommet du cône mais ensuite la base reste toujours sous notre cône et on peut toujours pas la réduire en un point ?

[Ben314]

Je pense que je viens de comprendre ton problème : en fait tu parle d'homotopie avec point de base (fixe) comme lorsque l'on construit le groupe fondamental d'un espace topologique alors que je te parle d'homotopie sans point de base, c'est à dire que je regarde un lacet comme une application continue de 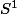dans l'espace considéré et une homotopie comme une application de 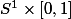dans l'espace en question (donc pour reprendre l'exemple de l'élastique, je fait remonter tout l'élastique au sommet du cône)

Je te laisse vérifier à titre d'exercice que ça ne change rien, c'est à dire que, si tu as un lacet homotope à un point dans le sens que j'emploie, alors il est aussi homotope à un point via une homotopie qui préserve le point de base du lacet.

[Archytas]

[img][IMG]http://img15.hostingpics.net/pics/771691IMG0657.jpg[/img][/img]

En gros je comprends pourquoi le petit lacet rouge peut se contracter mais le lacet bleu lui je ne vois pas ce que la présence du cône change, on peut en gros "tirer" notre lacet à partir de O partout sur le cône mais je vois pas ce que ça change sur le cercle bleu

[Ben314]

On met la base du cône à la hauteur 0 et le sommet à la hauteur 1.
A l'instant t (entre 0 et 1) tu considère le lacet gamma_t qui
- Part de O
- Monte le long du segment [OS] jusqu'à atteindre la hauteur t.
- Fait le tour complet du cercle correspondant au cercle bleu de départ mais situé à la hauteur t (c'est à dire l'image du cercle de départ par l'homothétie de centre S et de rapport 1-t)
- Redescend le long du segment [OS] pour retourner au point O.

La fonction (t,s)->gamma_t(s) te donne une homotopie préservant O entre ton cercle bleu à la base du cône (pour t=0) et le lacet faisant uniquement un aller-retour sur le segment [OS] (pour t=1). Ce dernier lacet est évidement homotope au lacet constant égal à O. (et tu constate que l'homotopie (t,s)->gamma_t(s) préservant O est déduite de façon immédiate de l'homotopie ne préservant pas O consistant à faire "monter" tout le cercle bleu vers le sommet S du cône)

Dit en terme imagé, tu "fait passer" ton élastique par le sommet S pour le faire redescendre le long du segment [OS].

[Archytas]

Ahhhh d'accord !! Donc il y a une infinité de petit cônes dans le gros cône ! Donc mon dessin est pas du tout juste j'ai oublié plein de cône tangents ! En fait si on appelle A tous les cercles tangents notre cône est Ax[0;1]/Ax{1} ! Moi je pensais que c'était A U Sx[0;1]/Sx{1}
Avec S le cercle extérieur !
Ok je vois très bien maintenant le caractère locale ! On a besoin du haut du cône pour tout homotoper ! Merci pour vos explication et pardon pour ma lenteur
Et donc le fait qu'on ne puisse pas trouver de revêtement universel vient de O ? Mais je vois pas bien pourquoi on peut pas en trouver à cause de ça

[Ben314]

Ben si, justement, vu que le cône C en question est connexe par arcs et semi localement simplement connexe, le "théorème d'existence" te dit qu'il admet bien un revêtement universel.
Sauf que ça a pas vraiment d'intérêt vu que, comme en plus le cône en question est simplement connexe, son revêtement universel, ben c'est lui même et c'est tout...

Et effectivement, j'ai pas pensé à préciser que le terme de "cône" que j'employais se référait à la définition topologique du terme cône (i.e. Ax[0,1]/Ax{1} comme tu le dit) et pas à la définition "géométrie élémentaire" avec une base qui est un unique cercle.