Espace complet !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Mar 2009, 11:42
par barbu23 » 01 Mar 2009, 11:42
Bonjour à toutes et à tous :
Je voudrai savoir si :
 = \{ \hspace{2cm} (u_{n})_{n \geq 0} \in \mathbb{R}^{\mathbb{N}} \hspace{2cm}~~ |\hspace{2cm} ~~ \displaystyle \sum_{n \geq 0} |u_{n}|^{2} < + \infty \} \hspace{2cm}$)
est complet ou non ? Si oui, comment le demontrer ?
Merci infiniment ! :we:
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 01 Mar 2009, 12:04
par Arkhnor » 01 Mar 2009, 12:04
Salut.
Il est bien complet.
Pour le montrer, prend une suite de Cauchy
})_r)
dans
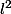
, et montre que les suites
}_n)_r)
sont de Cauchy pour

fixé.
Tu obtiens donc une suite
_n)
définie par
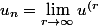}_n)
.
Il faut ensuite montrer que cette suite appartient à
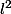
et que la suite
})_r)
converge bien vers
_n)
au sens de la norme
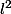
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 01 Mar 2009, 12:22
par ffpower » 01 Mar 2009, 12:22
Cela dit,il aurait fallu quand meme preciser la norme sur ton espac,meme si on se doute que c est la norme l2.Car si on prenait la norme infinie,ca serait ballot lol..
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Mar 2009, 12:30
par barbu23 » 01 Mar 2009, 12:30
Oui la norme , c'est :
_{n \geq 0}|| = \sqrt{} = \displaystyle \sum_{n \geq 0} u_{n} \overline{u_{n} $)
Merci à "ffpower" et à "Arkhnor" pour toutes ces precisions !
Je vais essayer d'appliquer tes expliquations "Arkhnor" !
Merci encore une fois ! :we:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 01 Mar 2009, 12:34
par kazeriahm » 01 Mar 2009, 12:34
je croyais que tu maitrisais les espaces l^2 Pablo ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Mar 2009, 12:36
par barbu23 » 01 Mar 2009, 12:36
Pas trop ! :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 282 invités