salut
un produit qlq des espaces de baire est il un espace de baire ?
est ce quelqu'un peut m'aider sur l'origine de la theoreme de baire comment etait le developpement du theoreme
merci
Espace de baire
7 messages
- Page 1 sur 1
Bonjour,
j'espère ne pas trop m'avancer en disant que : OUI.
Un ouvert d'un espace produit est constitué d'un nombre fini d'ouverts complétés par le produit des autres espaces...pour la rédaction, et en prenant un cas plus général, essayons de voir si la propriété de Baire est vérifiée pour des produits quelconque d'ouverts (qui n'est pas en général ouvert):
Si les_{i\in I}) sont des espaces de Baire et pour tout
sont des espaces de Baire et pour tout 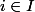 les
les _n) sont des ouverts denses de
sont des ouverts denses de  alors tout d'abord, il est évident que
alors tout d'abord, il est évident que 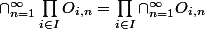 , il faut trouver le plus petit fermé qui le contient.
, il faut trouver le plus petit fermé qui le contient.
D'après ce qui a été écrit au premier paragraphe, on en déduit qu'un fermé d'un espace produit est constitué d'un produit fini de fermés et complété par des espaces vides (ou alors c'est l'espace produit tout entier) et comme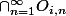 est dense dans
est dense dans  aucun des fermés constitués de produits finis de fermés ne peut contenir
aucun des fermés constitués de produits finis de fermés ne peut contenir 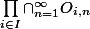 dont la fermeture est donc
dont la fermeture est donc 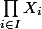 qui est donc de Baire.
qui est donc de Baire.
j'espère ne pas trop m'avancer en disant que : OUI.
Un ouvert d'un espace produit est constitué d'un nombre fini d'ouverts complétés par le produit des autres espaces...pour la rédaction, et en prenant un cas plus général, essayons de voir si la propriété de Baire est vérifiée pour des produits quelconque d'ouverts (qui n'est pas en général ouvert):
Si les
D'après ce qui a été écrit au premier paragraphe, on en déduit qu'un fermé d'un espace produit est constitué d'un produit fini de fermés et complété par des espaces vides (ou alors c'est l'espace produit tout entier) et comme
salut
mais un ferme dans un espace topologique produit n'est pas comme vous avez citez.par exemple pour que (x,y) appartienne au complémantaire de A*B il suffit que x ne soit pas dans A ou que y ne soit pas dans B.Et on dit qu'un produit qlq de ferme est un ferme.
mais on peut utiliser le fait que l'adherence de produit est le produit des adherences et c'est dans ce cas l'espace tout entier.je crois qu'il fait marcher.
mais un ferme dans un espace topologique produit n'est pas comme vous avez citez.par exemple pour que (x,y) appartienne au complémantaire de A*B il suffit que x ne soit pas dans A ou que y ne soit pas dans B.Et on dit qu'un produit qlq de ferme est un ferme.
mais on peut utiliser le fait que l'adherence de produit est le produit des adherences et c'est dans ce cas l'espace tout entier.je crois qu'il fait marcher.
*=le produit.
montrons que le produit des adherencs est un ferme. soit x=(xi) un elément du complémentaire des produits des adherences donc il existe i tel que xi est dans le complementaire de l'adherence de Ai qui est un ouvert alors il existe un voisinage Vi de xi inclus dans le complémentaire de Ai,or le produit de Vi complété par l'espace est un voisinage de x et il est inclus dans le complémentaire des produits des adherences d'ou la fermeture de produit.
on sait que *Ai est inclus dans produit des adherences de Ai alors le produit des adherences de Ai contient la fermeture de *Ai
l'autre sens on prend un point dans la fermeture de *Ai et son voisinage qlq l'intersection est non vide
montrons que le produit des adherencs est un ferme. soit x=(xi) un elément du complémentaire des produits des adherences donc il existe i tel que xi est dans le complementaire de l'adherence de Ai qui est un ouvert alors il existe un voisinage Vi de xi inclus dans le complémentaire de Ai,or le produit de Vi complété par l'espace est un voisinage de x et il est inclus dans le complémentaire des produits des adherences d'ou la fermeture de produit.
on sait que *Ai est inclus dans produit des adherences de Ai alors le produit des adherences de Ai contient la fermeture de *Ai
l'autre sens on prend un point dans la fermeture de *Ai et son voisinage qlq l'intersection est non vide
Bonjour,
tu as donc montrer (si j'ai bien compris) au début dans ton avant dernier message que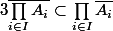 en montrant que
en montrant que 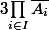 est un fermé qui contient
est un fermé qui contient 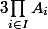 .
.
Par contre pour l'inclusion réciproque:
il faudrait plutôt prendre un point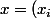_{i\in I}) dans le produit des adhérences de
dans le produit des adhérences de  :
: 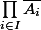 et
et  un voisinage ouvert de
un voisinage ouvert de  ; il existe donc
; il existe donc _{i\in I}) des ouverts tels que
des ouverts tels que 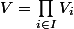 et
et 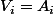 sauf pour un nombre fini de
sauf pour un nombre fini de  et comme
et comme 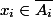 ,
, \cap\(\prod\limits_{i\in I}A_i\)\neq\emptyset) (axiome du choix) donc
(axiome du choix) donc 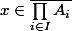 et on a l'inclusion réciproque.
et on a l'inclusion réciproque.
Avec tout ceci on sait maintenant que le produit des adhérences est égal à l'adhérence des produits (***) et on peut conclure :
Soient_{n\geq 0}) des ouverts denses de
des ouverts denses de 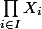 . On a pour tout entier
. On a pour tout entier 
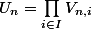 et les
et les 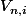 sont des ouverts et
sont des ouverts et 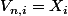 sauf pour un nombre fini de
sauf pour un nombre fini de  et il n'y a plus qu'à montrer grâce à (***) que
et il n'y a plus qu'à montrer grâce à (***) que 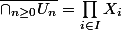
tu as donc montrer (si j'ai bien compris) au début dans ton avant dernier message que
Par contre pour l'inclusion réciproque:
l'autre sens on prend un point dans la fermeture de *Ai et son voisinage qlq l'intersection est non vide
il faudrait plutôt prendre un point
Avec tout ceci on sait maintenant que le produit des adhérences est égal à l'adhérence des produits (***) et on peut conclure :
Soient
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
