[Topic dupliqué ] Espace de Baire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 11 Nov 2010, 15:36
Bonjour à tous : :happy3:
Je bute sur une moitié de questions de l'exo suivant, le voiçi :
Soit
un epsace topologique.
Prouver que les deux assertions suivantes sont equivalentes :
- Pour toute suite de fermés
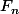
d'interieur vide,
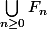
est d'interieur vide.
- Pour toute suite d'ouverts
denses dans
, alors
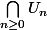
est dense dans
.
On dit que
est un espace de Baire.
Montrer que tout ouvert
d'un espace de Baire est de Baire.
On veut montrer que
( munie de la topologie usuelle ) est de Baire.
Soit
_{n \geq 1} $)
une suite d'ouverts denses dans
et
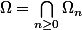
- Montrer que
est dense dans
si tout intervalle
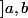
rencontre
- Soit
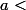
, montrer qu'il existe
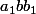
tels que
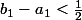
et
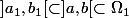
- Montrer qu'il existe deux suites
_{n \geq 1} $)
et
_{n \geq 1} $)
telles que
et
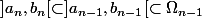
pour
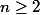
-En deduire que
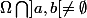
Merci d'avance. :happy3:
-
Ben314
- Le Ben
- Messages: 21696
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 11 Nov 2010, 15:55
Plutot que de recopier ma remarque (visiblement, tu n'as pas changé l'énoncé donc il est toujours faux) je te donne le lien pour relire l'autre discution (en mode "impression") :
http://www.maths-forum.com/printthread.php?t=112704Mais je ne sais pas comment tu doit faire pour modifier ton post et enlever la balise MimeTeX que tu as mis et qui à fait "planter" le truc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 11 Nov 2010, 16:09
N.B :
 $)
est le complementaire d'une partie
de
.
Pour la première question :
Soit
_{n \geq 1} $)
une suite d'ouverts de
tels que
:
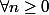
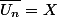
On pose :
:
 $)
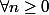
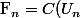On a :
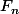
est un fermé de
pour tout
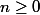
tel que
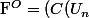^O =C(\overline{U_{n}}) = C(E) = \emptyset $)
Par hypothèse :
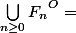
c'est à dire :
}^O = \emptyset $)
C'est à dire :
}^O = \emptyset $)
C'est à dire :
 = \emptyset $)
C'est à dire :
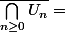
Inversement :
Soit
_{n \geq 0} $)
une suite de fermés de
tels que
:
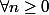
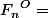
On pose :
 $)
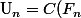pour tout
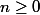
Alors :
_{n \geq 0} $)
est une suite d'ouverts tel que
:
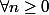
 } = C({F_{n}}^O) = C(\emptyset) = X $)
Par hypothèse :
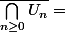
C'est à dire :
} = X $)
C'esy à dire :
} = X $)
C'esy à dire :
 = X $)
C'est à dire :
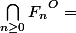
Maintenant, pour la question suivante, pourriez vous m'aider à montrer que pour tout ouvert d'un espace de Baire est de Baire ?
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 11 Nov 2010, 16:28
On continue sur ce topic Ben314 :happy3:
Il y'avait plusieurs fautes de frappes dans l'autre l'enoncé de le fil precedent, maintenant c'est corrigé. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 11 Nov 2010, 17:27
Soit
un ouvert de
qui est un espace de Baire.
Montrons que
est un espace de Baire.
Donc, nous allons montrer que pout toute suite d'ouverts
_{n \geq 0} $)
denses dans
, alors :
.
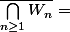
Soit
une suite d'ouverts tel que
:
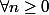
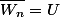
On a :
:
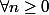
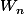
est un ouvert de
, alors
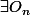
une suite d'ouverts de
tels que
:
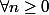
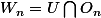
On a :
Est ce que :
?
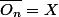
MErci d'avance. :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
