Le première question découle des définitions: on montre facilement que le complémentaire d'un fermé d'intérieur vide est un ouvert dense.
La seconde question se fait avec les ouverts.
Pour la question suivante, j'aurai tendence à dire qu'il faut prendre un voisinage de b dans
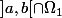
, comme on prend des voisinages de l'infini dans R.
Cela dit, je n'ai jamais fait ça pour un autre point que l'infini avant (b n'est pas dans l'ouvert, alors prendre un voisinage de b peut paraitre bizarre)
...
mais oui c'est bon, la base d'ouvert contient bien ce type de voisinage puisqu'il s'agit de la topologie induite sur l'ouvert
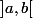
edit : ah non c'est
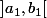
qu'il faut trouver. ça me semble simple du coup (et moins louche puisque le voisinage de b yavais peu ed chance de le faire rentrer dans
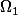
)
Donc prendre un point d'
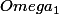
, prendre la partie connexe de ce point puis une boule le contenant, dans la partie connexe, que l'on retréciera pour avoir le rayon demandé.
