Equivalent et theoreme de Cesaro

par **praud** » 11 Oct 2007, 20:51

on sait que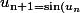

et

.J'ai calculé que

et que

On me demande de un equivalent en l'infini de

en utilisant le theoreme de Cesaro.

par **klevia** » 11 Oct 2007, 21:58

t'es sur de ta 2ème limite ?

1/Un²-1/Un= (1-Un)/Un² d'où lim 1-Un = 1
lim Un²=0 d'ou lim 1/Un²-1/Un= inf !!! ????

je veux bien que tu vérifies ...

par **praud** » 11 Oct 2007, 22:18

Ma limite est sure.Je l'ai obtenue en faisant un DL.

par **yos** » 11 Oct 2007, 22:29

Il faut chercher la limite de

puis appliquer Cesaro.

par **klevia** » 11 Oct 2007, 22:29

Alors je comprends pas ... Je suis désolé je peux pas t'aider, je suis pas assez forte ...
Pour moi lim 1/un²-1/un= inf

je suis formelle aussi... tant pis ...

par **klevia** » 11 Oct 2007, 22:30

je viens de lire le message de yos , c'est pas du tout la même limite !!!
je comprends mieux !!!

par **praud** » 11 Oct 2007, 22:39

On a

or

somme telescopique).
Donc

.
Comment conclure?

par **yos** » 11 Oct 2007, 22:43

1/u_n^2~n/3 donc u_n~(3/n)^(1/2)

par **SimonB** » 12 Oct 2007, 06:16

C'est d'ailleurs une méthode qui marche couramment pour les suites définies par un terme et une récurrence

avec f continue. On cherche la limite de la suite, on cherche

tel que

avec L non nulle, et on conclut grâce à Cesàro.

Equivalent et theoreme de Cesaro

equivalent et theoreme de Cesaro

bizzare...

désolé ...

re

Qui est en ligne