Equivalence d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 14:35
par akiwhite » 09 Jan 2020, 14:35
Bonjour, bonsoir,
Je dois simplifier la suite suivante :
)
avec des équivalences.
Je trouve alors
\pi - \frac{n}{n + 1}\pi) = sin(-\frac{n}{n + 1}\pi) \times ( -1^{n+1}))
On obtient alors avec les exemples fondamentaux
 + o(\frac{n}{n + 1}))
Je me demande alors si je peux encore simplifier cette suite.
Merci d'avance pour vos réponses,
Akiwhite
Modifié en dernier par
akiwhite le 09 Jan 2020, 15:13, modifié 1 fois.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 09 Jan 2020, 15:00
par tournesol » 09 Jan 2020, 15:00
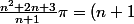\pi+\frac{2\pi}{n+1})
Donc
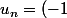^{n+1}sin(\frac{2\pi}{n+1})=(-1)^{n+1}sin(\frac{2\pi}{n}+o(\frac{1}{n}))=(-1)^{n+1}\frac{2\pi}{n}+o(\frac{1}{n}))
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 09 Jan 2020, 15:05
par GaBuZoMeu » 09 Jan 2020, 15:05
Hum... Exercice fait à la place du questionneur !
Il eut mieux valu se contenter de lui signaler son erreur de calcul.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 15:12
par akiwhite » 09 Jan 2020, 15:12
Pardon je me suis trompé en écrivant l'énoncé ! C'est n² + n + 1
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 15:15
par akiwhite » 09 Jan 2020, 15:15
tournesol a écrit: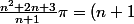\pi+\frac{2\pi}{n+1})
Donc
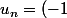^{n+1}sin(\frac{2\pi}{n+1})=(-1)^{n+1}sin(\frac{2\pi}{n}+o(\frac{1}{n}))=(-1)^{n+1}\frac{2\pi}{n}+o(\frac{1}{n}))
Est-ce possible d'écrire
))
car dans mon cours l'exemple fondamental du sinus est
 = U_n + o(U_n))
avec lim Un =0
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 09 Jan 2020, 15:18
par GaBuZoMeu » 09 Jan 2020, 15:18
Ton calcul ne va pas parce que

ne tend pas vers 0. Mais par contre, ça se rapproche de plus en plus d'un entier ....
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 09 Jan 2020, 15:25
par tournesol » 09 Jan 2020, 15:25
J'ai donné la réponse car l'étudiant s'est investi dans son exo en proposant une solution .
Puisqu'il s'est aussi trompé dans l'enoncé , elle lui servira d'exemple .
Cependant je suis d'accord avec toi GaBuZoMeu.
Modifié en dernier par
tournesol le 09 Jan 2020, 15:26, modifié 1 fois.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 15:26
par akiwhite » 09 Jan 2020, 15:26
GaBuZoMeu a écrit:Ton calcul ne va pas parce que

ne tend pas vers 0. Mais par contre, ça se rapproche de plus en plus d'un entier ....
Effectivement ...
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 09 Jan 2020, 15:40
par GaBuZoMeu » 09 Jan 2020, 15:40
Et donc, vois-tu quoi faire ?
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 16:31
par akiwhite » 09 Jan 2020, 16:31
Devrait-on obtenir ceci ?
\pi - \frac{n}{n + 1}\pi) = sin((n)\pi + \frac{1}{n + 1}\pi) = ((-1)^{n}) ((\frac{1}{n + 1}\pi) + o(\frac{1}{n}\pi)))
D'ailleurs faut il conserver les pi comme je l'ai fait ?
Modifié en dernier par
akiwhite le 09 Jan 2020, 18:37, modifié 4 fois.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 16:32
par akiwhite » 09 Jan 2020, 16:32
J'ai une autre petite question : comment calculer la limite d'un petit o ? Est elle toujours égale à 0 ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 09 Jan 2020, 16:35
par GaBuZoMeu » 09 Jan 2020, 16:35
Euh... Tu es sûr de
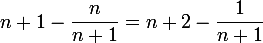
?
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 16:38
par akiwhite » 09 Jan 2020, 16:38
GaBuZoMeu a écrit:Euh... Tu es sûr de
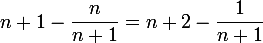
?
Non pas du tout

C'est corrigé
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 09 Jan 2020, 16:39
par GaBuZoMeu » 09 Jan 2020, 16:39
Ça ne va toujours pas. Soit plus attentif !
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 16:45
par akiwhite » 09 Jan 2020, 16:45
GaBuZoMeu a écrit:Ça ne va toujours pas. Soit plus attentif !
Alala j'ai honte

-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 09 Jan 2020, 16:56
par GaBuZoMeu » 09 Jan 2020, 16:56
Bon, maintenant que les étourderies sont corrigées, on en est à
= (-1)^n\sin\left(\dfrac1{n+1}\,\pi\right))
et maintenant on peut utiliser un équivalent de
)
quand
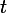
tend vers 0.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 17:00
par akiwhite » 09 Jan 2020, 17:00
GaBuZoMeu a écrit:Bon, maintenant que les étourderies sont corrigées, on en est à
= (-1)^n\sin\left(\dfrac1{n+1}\,\pi\right))
et maintenant on peut utiliser un équivalent de
)
quand
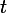
tend vers 0.
Oui c'est deja fait !
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 09 Jan 2020, 17:02
par tournesol » 09 Jan 2020, 17:02
tu peux avoir honte car
+1}{n+1}=n+\frac{1}{n+1})
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 09 Jan 2020, 17:27
par GaBuZoMeu » 09 Jan 2020, 17:27
akiwhite a écrit:Oui c'est deja fait !
Je ne suis pas sûr que tu aies simplifié un max. Il ne te reste pas un

au dénominateur ? Tu peux faire avec deux symboles de moins.
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 09 Jan 2020, 17:42
par akiwhite » 09 Jan 2020, 17:42
On peut simplifier par 1/n, merci beaucoup pour ton aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
ne tend pas vers 0. Mais par contre, ça se rapproche de plus en plus d'un entier ....

quand
tend vers 0.