Re: Equivalence, suite

[akiwhite]

Bonjour, bonsoir,

Je bloque sur les questions suivantes :

Soit Sn une suite de réels de limite 0 et tq : .

1) On suppose que (Sn) est décroissante, montrer que

2) En considérant la suite , prouver que ce résultat est en défaut si (Sn) n'est pas décroissante.

1) Je n'ai aucune piste ... !
2) A défaut d'utiliser la réponse 1) j'ai tenté de prendre de cette suite et de soustraire au rang n+1 mais je ne trouve rien de concluant.

Merci pour votre aide,

Akiwhite

[LB2]

Bonjour,

1) Reviens à la définition de l'équivalent en l'écrivant avec un certain quotient qui tend vers 1.
L'idée est d'utiliser la décroissance de la suite Sn, pour encadrer 2nSn par des suites bien choisies qui tendent toutes les deux vers 1. On retrouve la même idée dans les intégrales de Wallis. Le point important étant qu'en général pour une suite u_n, il n'y a aucune raison que u_{n+1} et u_n soient équivalents (penser à une suite géométrique).

2) La philosophie de l'exercice : on n'additionne jamais les équivalents.
Calcule Sn+S(n+1) dans un premier temps, puis calcule un équivalent simple de cette quantité (en utilisant les D.L. en 0 avec la variable h=1/n)
Ensuite, est-ce que (Sn) est équivalent à 1/(2n) ? Pourquoi ?

Conclusion

[akiwhite]

Merci pour ta réponse,
mais malheureusement j'ai du mal à trouver un encardrement pour Sn et ainsi encadrer 2nSn !

Et je ne connais pas encore la méthode des DL pour la question deux ^^

[akiwhite]

Je pense qu'on peut déja avoir 1/2n <= Sn

[LB2]

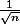
Pour la 2., factorise la parenthèse par pour commencer.

[tournesol]

le plus simple est d'utiliser la caractérisation de l'équivalence suivante :
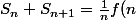avec lim f(n)=1
par décroissance , on en déduit
et donc
Il ne te reste plus qu'à montrer que 2nSn tend vers 1 .