Equivalence en ln

[Florix]

Bonjour,

J'ai une question toute bête que j'arrive pas à résoudre. Je cherche un équivalent en +oo de la formule suivante :

A = [ ln ( n + 1 ) ] ( n + 1/2 ) + [ ln ( n ) ] ( - n - 1/2 ) - 1

Sachant que l'équivalence n'est pas compatible avec la somme comment faire ? je voudrais transformer A en un produit de facteurs, en factorisant par ln par exemple mais impossible de relier ln à ln ( n + 1 ) sans passer par une somme, ce qui ne m'avance pas pour la recherche de l'équivalence. On serait tenté de dire n + 1 est équivalent à n mais après on somme des équivalences donc c'est faux.

Comment faire ?

[abcd22]

Bonsoir,
Tu peux poser x = 1/n, comme ça tu te ramènes à trouver un équivalent en 0, ce que tu peux faire avec un développement limité.

[Florix]

Ouais mais c'est en +oo que je cherche !

[abcd22]

Quand n tend vers + l'infini x = 1/n tend vers 0, donc on fait un développement limité quand x tend vers 0 de l'expression obtenue en remplaçant n par 1/x, à un ordre assez grand pour qu'on n'ait pas juste un petit o de quelque chose, on prend le premier terme du développement limité, on reremplace x par 1/n et ça donne l'équivalent qu'on cherchait.

Si tu veux tu peux aussi écrire ln(n+1) = ln (n(1+1/n)) = ln n + ln (1 +1/n), il y a des simplifications et ensuite on utilise le développement limité de ln(1+x) en 0 pour écrire ln(1+1/n) = 1/n - ... + o( ...), avec les o on peut additionner, on choisit l'ordre assez grand pour que tout ne se simplifie pas et on a l'équivalent directement. C'est pareil que ce que j'ai dit avant sauf qu'on ne dit pas qu'on fait un changement de variable en fait.

[Florix]

Bonjour,

J'ai finalement trouver que A était équivalent en +oo ! Merci abcd22 :++:

Cependant cela me pose un problème pour la question d'après, car en fait A = Xn - Xn+1 . La question est "En déduire que la suite (xn) converge.

Donc si on a Xn - Xn+1 equivalent à 1 en +oo , cela veut dire que Xn est équivalent en +oo à Xn+1, et que donc la suite est stationnaire à partir d'un certain rang quand n tend vers +oo

Cela suffit-il à justifier que la suite converge ?

NB : la suite Xn = somme de k=1 à n de ln k - n ln n + n - 1/2 ln n

[abcd22]

Rebonjour, tu as dû faire une erreur dans les calculs, j'avais quelque chose en 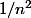, avec un DL à l'ordre 3 du ln, parce qu'à l'ordre 1 ou 2 tout se simplifiait. Avec on peut écrire que et la série converge grâce à l'équivalent (ne pas oublier de parler de la positivité), donc converge.

Si on a une suite telle que la suite diverge, en utilisant la même technique que plus haut.