Raisonnement (Equivalence)

[beagle]

de prime abord
x²+x+1 = 0 j'ai pas de solution pour x réel
et lorsque l'on passe à x^3 ton égalité admet déjà x=0 comme solution
première arnaque

ensuite faut voir pourquoi en solution de complexes on -racine cubique de -1, et -1^2/3
et que justement tu nous la joue sur le 1 en puissance 3

[hdci]

de prime abord
x²+x+1 = 0 j'ai pas de solution pour x réel

C'est vrai, mais ce n'est pas pour cela que mon raisonnement est faux (d'ailleurs est-il faux ?)
J'irai même jusqu'à dire qu'un théoricien du complot ne comprenant rien à la logique s'emparerait de cette démonstration pour prouver qu'on nous ment, que les maths sont extrêmement contradictoires...

et lorsque l'on passe à x^3 ton égalité admet déjà x=0 comme solution
première arnaque

Absolument pas : à aucun moment je ne prétends que est solution et comme je ne divise jamais par il n'y a absolument aucun problème (même s'i lest vrai que 0 est solution de , mais il ne l'est pas de )

ensuite faut voir pourquoi en solution de complexes on -racine cubique de -1,
et que justement tu nous la joue sur le 1 en puissance 3

Dans les complexe admet 3 solutions distinctes, dont deux complexes que je vais noter et (de module 1 et d'argument pour , pour )
Donc la ligne est fausse dans les complexes (mais totalement vraie dans les réels)

...Et il se trouve que et sont solutions de l'équation :

[beagle]

hdci je n'ai pas dit que j'avais trouvé,
c'est d'ailleurs assez sympa comme truc
J'ai dit je cherche où il ya des trucs bizarres
et passer de pas de solution à une solution est un endroit déjà suspect, mais j'ai bien compris que c'est pas x =0 la solution
Quant aux complexes je n'y connais absolument plus rien de rien
Malheureusement le boulot reprend et je regarde cela entre deux trucs.
mais effectivement c'est bien foutu!!!!

[beagle]

Bon alors lorsqu'on multiplie par x,
comme il n' ya pas de x existant on ne devrait pas pouvoir multiplier par x qui n'existe pas.

s'il existe un x solution, alors je peux multiplier par x,
si x solution existe , je trouve x=1
or 1 n'est pas solution puisque amène 1 +1 +1 = 0
condradiction avec il existe un x
donc il n'existe pas de x solution

c'est diabolique ce truc!
tu démontres sans passer par la résolution de l'équation de second degré que s'il y avait une solution x, alors on aboutirait à une contradiction, et donc cette équation n'a pas de solution,
démontré par l'absurde ou la contraposée je ne sais en effet pas les différencier.

[hdci]

Pas mal ! C'est effectivement l'idée générale : SI 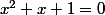avait une solution dans , ALORS .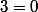

Le raisonnement est 100% fiable : ce n'est que l'utilisation du résultat qui ne l'est pas : croire qu'on a montré que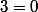 , alors qu'en fait, on a démontré que

D'un point de vue logique : le raisonnement est basé sur


C'est une tautologie : une proposition toujours vraie, quelles que soient les valeurs de vérité de A, B ou C. Pour les sceptiques, utilisez les tables de vérité pour montrer cela...

Finalement, on utilise le principe que le raisonnnement d'implication est vrai quand la conclusion est vraie, ou quand l'hypothèse est fausse. Ici la conclusion est manifestement fausse, donc l'hypothèse ne peut pas être vraie.

Pour en revenir sur les complexes : comme indiqué un peu avant, il y a trois racines complexes (dont une seule réelle) au polynôme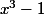 ce qui fait que l'implication est fausse (la conclusion d'une implication est une condition nécessaire pour l'hypothèse, or là la condition n'est pas nécessaire puisqu'il existe des valeurs admissibles différentes de 1) ; elle est sufisante, ce qui est vrai c'est l'implication réciproque ).

Dans le raisonnement, attention à cette phrase

Bon alors lorsqu'on multiplie par x,
comme il n' ya pas de x existant on ne devrait pas pouvoir multiplier par x qui n'existe pas.

(On peut toujours multiplier par , le résultat étant une proposition soit vraie soit fausse.)

Au vu de la démonstration on ne sait pas qu'il n'y a pas de existant (on ne le sait que parce qu'on connaît le discriminant, ou parce qu'on sait étudier les variations du polynôme et trouver son minimum, etc.), mais sans le savoir...
Or une démonstration ne peux pas être "correcte" sans savoir l'existence d'un théorème, et "incorrecte" en connaissant ledit théorème.

Par contre, ce phrasé est totalement correct

s'il existe un x solution, alors je peux multiplier par x,
si x solution existe , je trouve x=1
or 1 n'est pas solution puisque amène 1 +1 +1 = 0
condradiction avec il existe un x
donc il n'existe pas de x solution

Et c'est un raisonnement par l'absurde (on suppose que l'hypothèse est vraie, on arrive à une contradiction). Ou ce qui revient ici au même et fausse donc fausse.

Une contraposée, c'est quand on veut montrer que est vraie, et pour cela on montre que
(Exemple : "il pleut, donc il y a des nuages" est identique à il n'y a pas de nuage, donc il ne pleut pas")

[beagle]

"Bon alors lorsqu'on multiplie par x,
comme il n' ya pas de x existant on ne devrait pas pouvoir multiplier par x qui n'existe pas."

cette phrase est fausse, mais c'est elle qui m'a mis sur le chemin.

Dans tous les bons tours de magie ce qui bluffe c'est d'orienter les sens, la raison vers un leurre qui masque le tour. Ici le leurre c'est que tu tournes en rond à chercher un calcul interdit, alors que les calculs sont bons.
le truc est ailleurs
Oui c'est superbe.
En plus de bien illustrer ce que tu voulais faire passer.

[Ben314]

C'est un grand classique et il n'y a aucune erreur de raisonnement où que ce soit :

Tu montre que, SI un réel vérifie x²+x+1=0 ALORS x=1.
Et le fait que x=1 ne vérifie pas l'équation en question, ben tout ce que ça prouve, c'est qu'il n'y a pas de réel solution de l'équation.

Et pour préciser un peu plus, le raisonnement consiste à dire que l'équation de départ est équivalente à une certaine équation A=B et qu'elle est aussi presque (*) équivalente à une certaine équation B=C.
Par contre, le truc trivial, c'est que (A=B et B=C) ça implique effectivement que A=C mais ce n'est bien évidement pas une équivalence et on le voit parfaitement bien dans les calculs où, si on prend x=1, on a effectivement A=C, mais on n'a ni A=B, ni B=C.

(*) Sauf pour x=0

[Pseuda]

L'interdiction d'utiliser l'implique dans les démonstrations vient du fait que l'implication est vraie lorsque p est faux.
...
Donc de mon temps, l'utilisation au collège, au lycée de l'implication se faisait en prenant pour admis que p était vrai,
on ne faisait que du si p vrai, j'ai ou j'ai pas q?
Avec l'utilisation "normale" des logiciens de l'implique il faudrait préciser
Si p alors q et j'ai p vrai.

Bonsoir,

Ah c'est donc ça ! Merci Beagle. Sauf que, comme tu le dis, au lycée et au collège, le implique p=>q est toujours utilisé avec le sous-entendu que p est vraie (sinon, on n'écrit même pas p si p est fausse (d'ailleurs "p" est un raccourci de "p est vraie").
Dans le sens du "implique" puriste, on utilise "si..., alors... ", pour bien faire la distinction (si 2 droites sont parallèles, alors toute parallèle à l'une est parallèle à l'autre, le implique ici serait ... bizarre).
Si on va par là, A=>B ne veut rien dire. Ce qui a du sens, c'est A=>B est vraie. Rrrr.

Dans le supérieur, je le vois rarement dans ce sens-là. Cela peut être par exemple dans une phrase comme (A=>B) <=> C.

Je trouve que c'est du purisme qui embrouille plus que cela ne résoud de problème. Ou alors, il faudrait un autre terme qui signifie à la fois "p est vraie et p implique q". Mais comme la plupart du temps, quand on énonce une proposition, c'est sous-entendue qu'elle est vraie, comment faire le distinguo ? Par contre, dans p<=>q, le problème ne se pose pas, on ne suppose ni p ni q vraie ou fausse, en effet.

[hdci]

Je trouve que c'est du purisme qui embrouille plus que cela ne résoud de problème. Ou alors, il faudrait un autre terme qui signifie à la fois "p est vraie et p implique q". Mais comme la plupart du temps, quand on énonce une proposition, c'est sous-entendue qu'elle est vraie, comment faire le distinguo ? Par contre, dans p<=>q, le problème ne se pose pas, on ne suppose ni p ni q vraie ou fausse, en effet.

Je ne suis pas tout à fait d'accord : P=>Q est une proposition qui est soit vraie soit fausse.
Si elle est fausse, c'est que P est vraie et Q est fausse.
Sinon, c'est que Q est vraie peu importe la véracité de P.
Si on sait que P=>Q est vraie, et si on sait que P est vraie, on en déduit que Q est vraie. Mais bien entendu tout cela ne se dit pas, c'est trop long et c'est exactement ce que signifie P=>Q

Et pour finir quand on dit "théorème : P=>Q", cela signifie que la proposition P=>Q est vraie.

Exemple : " il pleut => y'a des nuages" est une phrase vraie (OK parfois les nuages sont loin parce qu'il y a du vent, mais admettons).
Je regarde par la fenêtre, et tiens je vois qu'il pleut : j'en déduis qu'il y a des nuages.
Le lendemain, tiens il ne pleut pas : je ne sais pas dire s'il y a des nuages.
Le surlendemain, je regarde le ciel et tiens il n'y a pas de nuage. Donc je sais qu'il ne pleut pas.

On peut tourner dans tous les sens, rajouter "si P est vraie alors Q est vraie" ou ne pas le rajouter, finalement cela ne change absolument rien ; pour le reste c'est juste une question de clarté (de compréhension, d'explication, de présentation, etc.).

[Pseuda]

Une démonstration rédigée de façon 100% formelle est forcément valide et un ordinateur peut le vérifier (il me semble que c'est ce que fait le logiciel COQ, mais je ne le connais pas).
Par contre, une telle démonstration (sauf dans des cas relativement simple) est rapidement illisible et c'est bien la rédaction claire et l'esprit humain comprenant le raisonnement et les "sous-entendus" qui peut en décider.

Il me semble que si on a pu formaliser à 100% une démonstration, c'est que le problème de sa validité ne se pose plus. Autrement dit, j'ai l'impression que ça va dans le sens : la démonstration est valide => on peut la formaliser à 100%, et non pas dans le sens : la démonstration est formalisée à 100% => elle est valide.

Je demande à voir quand même une telle démonstration.

[beagle]

Salut hdci, tu nous réexpliques le machin, mais ça c'est ok.
Le problème est quelle utilisation on fait, à quelle age quelle classe,
et avec quelle notion
comment on laisse rédiger les gamins.
est-il génant d'avoir des théorèmes qui s'écrivent avec de l'implique dès le collège, mais on n'utilise plus l'implique pour rédiger son problème particulier.
Si on supprime le signe implique, on empèche aussi d'écrire si A alors B. ?
Bref les notions de l'implique avec tables de vérité, à quelle age, quelle classe,
et on autorise on s'autorise quoi avant?

Donc moi on m'a dit les gamins doivent écrire
A donc B

Et n'est-il pas surprenant que l'équivalence ne pose aucun problème dans la rédaction, enfin pas le problème qs de l'implique, mais que de ce fait on enseigne (ou pas ?) l'équivalence sans dire que c'est si A alors B et si B alors a????

bref on apprend quoi a qui?

[Pseuda]

@hdci Ce que je veux dire par là avec le implique, c'est que quand on énonce une proposition "P", c'est sous-entendu qu'elle est vraie.

Mais quand on énonce la phrase P=>Q (bon c'est sous-entendue qu'elle est vraie), mais on a énoncé "P" dans cette phrase P=>Q, mais là, on ne suppose plus que P est vraie. Comment faire la distinction ?

[hdci]

@hdci Ce que je veux dire par là avec le implique, c'est que quand on énonce une proposition "P", c'est sous-entendu qu'elle est vraie.

Mais quand on énonce la phrase P=>Q, c'est sous-entendue qu'elle est vraie, mais on a énoncé "P" dans cette phrase, mais là, on ne suppose plus que P est vraie. Comment faire la distinction ?

C'est là le petit bémol : quand on énonce une proposition P on ne sait a priori pas dire si elle est vraie ou pas.
Quand on dit "SI P est vraie ALORS Q est vraie", on met bien une condition sur P : peut-être que P est fausse après tout.
Le seul truc "intangible", c'est : un axiome est une proposition décrétée comme VRAIE, un théorème est une proposition qu'on a démontré VRAIE (c'est-à-dire, vraie quelles que soient les vérités des ses constituants).

Il me semble que si on a pu formaliser à 100% une démonstration, c'est que le problème de sa validité ne se pose plus. Autrement dit, j'ai l'impression que ça va dans le sens : la démonstration est valide => on peut la formaliser à 100%, et non pas dans le sens : la démonstration est formalisée à 100% => elle est valide.

Je demande à voir quand même une telle démonstration.

Petit essai en théorie des ensembles.
Axiome A1 : (Il énonce qu'il y a au moins un ensemble dans l'univers)
X=X)"/>
Schéma d'axiomes S1(P) : il énonce qu'on peut définir un ensemble comme partie d'un autre ensemble qui vérifie une proposition donnée P


Théorème : il existe un ensemble vide :

Démonstration "formelle" : Proposition D

Vu comme ça c'est incompréhensible ; qui plus est il faut faire un peu de logique propositionnelle / logique du premier ordre et adopter les schémas de déduction, c'est un domaine dans lequel je n'ai qu'un peu de culture sans plus.
En décortiquant la logique du premier ordre : A1 dit qu'il existe un ensemble, c'est celui qu'on utilise dans S2 pour dire qu'il existe un sous-ensemble de cet ensemble dont chaque élément est différent de lui-même. Comme "chaque élément est différent de lui-même" est faux (seconde partie de l'équivalence de S2), cela signifie qu'il n'y a pas d'élément dans cette partie (première partie de l'équivalence de S2) .
La proposition D comporte ainsi une hypothèse qui est réputée vraie (axiomes) et une conclusion qui est vraie: le théorème est donc vrai dans le système d'axiomes

[Pseuda]

Je réponds à la 1ère objection. Il est dit dans la logique que si on ne précise pas si une proposition est vraie ou fausse, c'est sous-entendu qu'elle est vraie. Mais quand on énonce P=>Q, on n'a rien précisé sur P, donc on suppose que P est vraie.....................

[Pseuda]

@hdci A propos des ensembles vides. On considère 2 ensembles A et B, et P(A), P(B), les ensembles de leurs parties. L'ensemble vide est une partie de A comme de B. Question (que je me pose depuis longtemps) : l'ensemble vide partie de A est-il le même (ou non) que l'ensemble vide partie de B ? J'imagine que cette question n'est pas nouvelle.

[Pseuda]

Sinon pour le implique dans P=>Q au sens logique, je le vois surtout (et il doit certainement venir de là) comme la négation de : P est vraie et Q est fausse. Cela donne : P est fausse ou Q est vraie, soit : non P ou Q.

[hdci]

Sinon pour le implique dans P=>Q au sens logique, je le vois surtout (et il doit certainement venir de là) comme la négation de : P est vraie et Q est fausse. Cela donne : P est fausse ou Q est vraie, soit : non P ou Q.

Effectivement P=>Q a la même vérité que Non P ou Q
Il est à noter qu'en fait tous le opérateurs logiques (et, ou, implique, équivaut...) peuvent être générés à l'aide d'un seul opérateur, la "barre de scheffer", qui e, électronique est le "NAND" (non et)

@hdci A propos des ensembles vides. On considère 2 ensembles A et B, et P(A), P(B), les ensembles de leurs parties. L'ensemble vide est une partie de A comme de B. Question (que je me pose depuis longtemps) : l'ensemble vide partie de A est-il le même (ou non) que l'ensemble vide partie de B ? J'imagine que cette question n'est pas nouvelle.

En théorie des ensembles (que ce soit la théorie initiale de Cantor, qui avait une faille de taille celle de l'ensemble de tous les ensembles, ou la théorie ZFC qui pour le moment n'a pas montré de contradiction), l'un des axiomes dit que deux ensembles sont égaux ssi ils ont les mêmes éléments, cela s'exprime (en phrase prpopositionnelle)


Appliquer cela à deux ensembles V1 et V2 ne comportant aucun élément : l'équivalence équivalence est vraie (faux équivalent à faux) donc V1=V2 est vraie.
Bref, il n'y a bien qu'un seul ensemble vide : dans l'axiomatique choisie.

[Pseuda]

Ok merci pour l'ensemble vide. Mais j'aurais plutôt vu ça écrit comme ça :
.

Sinon pour l'objection soulevée avec P=>Q et P sous-entendue vraie, vous auriez pu répondre : mais (P=>Q) est un tout indissociable, on ne peut pas isoler P pour sous-entendre qu'elle est vraie.

Sinon je n'ai rien compris à la démonstration formellle (d'où sort S2 ?), peut-être demain.

[hdci]

Mais j'auraid plutôt vu ça écrit comme ça :

Oui c'est exact, mes parenthèses sont mal positionnées

[beagle]

Bon alors, nous (je ) en étions à le signe implique est une notion complexe, il faut l'enseigner tardivement.
Comme le "si … alors…" est une équivalence, il faut lutter contre son utilisation chez les jeunes.

Donc, nous sommes au collège, un carré ABCD, on va calculer la diagonale du carré.
L'élève écrit ceci:
D'après le théorème de Pythagore, si ABC est un triangle rectangle, alors le carré de l'hypoténuse AC est égale à …
Je suis le prof, sur la copie de l'élève j'entoure en rouge le "si ABC est un triangle rectangle",
et j'écrits: "et l'est-il?"
Je convoque les parents, vous savez votre fils s'il fait pas chanteur ou footballeur professionnel on risque de l'envoyer faire une prépa après le bac, je suis obligé de lui apprendre la rigueur...Je vous demandrais d'en faire autant à la maison.

C'est un peu comme ça qu'il faut faire?