Equidistribution et calcul de probabilité

[zaatour]

Bonsoir tout le monde,

J'ai une question à propos de l'équidistribution.

Je vais simplifier ma problématique: j'ai 1000 boules et 100 cases, quelle est la probabilité pour que les boules soient équi distribuées?

Merci d'avance!

Wajdi

[tournesol]

Avec 20 boules discernables numérotées de 1 à 20 et 4 cases discernables numérotées de 1 à 4 .
Nombre total de répartitions : 4 cases pour la boule 1 X 4 cases pour la boule 2 X ...= 4^20
Nombres de répartitions équidistribuées:
5 parmi 20 possibilités pour la case 1 X5 parmi 15 possibilités pour la case 2X...
Soit :
La probabilité d'obtenir une répartition équidistribuée est égale à :
Pour une évaluation numérique , faire calculer par programme son logarithme décimal
L'écriture scientifique est alors
La question a t-elle un rapport avec un exo de thermodynamique statistique ?

[zaatour]

Merci beaucoup, en effet oui j'utilise une théorie de la physique statistique, j'ai 1730 molécules et 1530 emplacement, et j'ai voulu voir la probabilité pour qu'elles soient équi réparties. Donc si j'ai bien compris j'utilise ta formule de La probabilité d'obtenir une répartition équidistribuée en remplaçant 20 par 1730 et 4 par 1530?

[tournesol]

Non car le 5 que j'utilises est egal à 20/4 et dans ton dernier cas , le nombre de cases ne divise pas le nombre de boules et l'equidistribution n'est possible que dans ce cas .

[tournesol]

Pour 2n boules dans 2 cases , la repartition la plus représentée est n boules par cases.
Pour 2n+1 boules dans 2 cases , les repartitions les plus représentées sont n dans une et n+1 dans l'autre .
Pour N boules dans n cases .
Soit la repartition k1 , ... , kn avec k1+...+kn=N
On choisit 2 cases i et j . On a la repartition ni , nj . Une répartition optimale(plus representée) de ces ni+nj boules est une de celles données précédemment selon la parite de ni+nj .
Il en résulte que dans ton cas , les repartitions optimales sont obtenues avec 1330 cases qui contiennent une boule et 200 qui en contiennent deux .
En résumé chaque emplacement doit contenir une ou deux molecules.

[zaatour]

MERCI beaucoup pour ta réponse

Dans mon cas j'aurais une somme de probabilité (le cas de n ou le cas de n+1) comment les écrire stp?

[zaatour]

L'objectif principal de ma question est de calculer l'entropie maximale pour que les molécules soient équi distribuées

[tournesol]

Le nombre de répartitions de n boules dans p cases telles que pour tout k il y ait 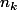boules dans la case k est égal à
Dans ton cas , le nombre de chaque répartition optimale est égal à
Comme il y a 200 façons parmi 1530 de choisir les cases qui contiennent 2 boules , il y a en tout répartitions optimales .
La probabilité que la répartition soit optimale est égale à
Si tu ne disposes pas de la puissance de calcul necessaire , tu calcules son log décimal et tu en deduis son écriture scientifique comme je te l'ai expliqué dans un de mes précédents messages .
tu dois trouver sauf erreur

[tournesol]

Remarque perso :quand on a des probas aussi petites , on ne devrait pas dire "évènement le plus probable" mais"évènement le moins impossible"

[zaatour]

Merci beaucoup!