2 équations 3 inconnues, est-ce possible ?

[Fada]

Bonjour,
Je ne suis pas très doué en math alors est-il possible de résoudre ce problème:

0,5x+3y+10z=100
x+y+z=100

x=?
y=?
z=?

Merci

[uztop]

Salut,

tu as plus d'inconnues que d'equations, tu ne pourras donc pas trouver une solution unique, mais une infinite de solutions.

[Pythales]

ou exprimer x et y en fonction de z (par exemple)

[uztop]

oui exactement, ca revient a avoir une infinite de solutions vu qu'il y a une inifinite de valeurs possibles pour z

[Clembou]

Bonjour,
Je ne suis pas très doué en math alors est-il possible de résoudre ce problème:

0,5x+3y+10z=100
x+y+z=100

x=?
y=?
z=?

Merci

Moi, je ne pense pas que ce système d'équations a une solution... Car la somme de trois réels ne peut pas être égal à la somme de ses trois mêmes réels multipliés chacun par des scalaires non nul et non égal à 1...

EDIT : Au temps pour moi ! J'ai trouvé une solution :++:

[Zweig]

Ce système admet effectivement une infinité de solutions. Détrompe-toi Clembou, x = 414/5, y = 81/5, z = 1 marche.

[jorro]

En effet il y a une infinité de solutions :++: :
Il suffit de fixer une variable réelle, par exemple , et il nous reste un système de 2 équations à 2 inconnues dépendantes du paramètre :

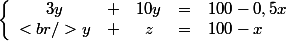là tu peux utiliser la méthode de ton choix ....


Bonne poursuite.

[touil abdelali]

Bonjour,
Je ne suis pas très doué en math alors est-il possible de résoudre ce problème:

0,5x+3y+10z=100
x+y+z=100

x=?
y=?
z=?

Merci

Je suis d'accord avec les amis car la solution de 0.5x+3y+10z=100 c'est de fixer une variable soit x ou y ou z

[Fada]

En effet,
J’ai oublié de préciser qu'il faut trouver des nombres entiers positifs.
J'ai trouvé un résultat sans formule unique mais avec une succession de tests d’une équation à deux inconnues en faisant des essais avec z=1 puis z=2 puis z=3 etc...et enfin, z=5 marche.
C’est laborieux et c’est pour cela que je vous ais sollicité dans le cas où il existerait une formule plus rapide.
En tout cas merci à tous pour vos réponses.

En isolant une inconnues (y par ex) j’obtiens une équation à deux inconnues et ensuite j’ai effectué les tests successifs :

1/2x+3y+10z=100
x+y+z=100

y=100-x-z

1/2x +3 (100-x-z) + 10z = 100
-------
x = 80 + 14/5 z

Test:
Avec z=5,
x=94
y=1

…OUF!

[Lapinou]

Bonjour comment tu a fait pour trouver x = 80 + 14/5 z?
Merci
J'ai une même équation que j'ai du mal a résoudre :
1/10x + 2y +5z=100
X+y+z=100

Merci