équation trigonometrique
22 messages
- Page 1 sur 2 - 1, 2
équation trigonometrique
Bonjour,
Je cherche à résoudre l'équation suivante:
a sin(x) + b = cot(x)
Merci d'avance pour votre aide!
Je cherche à résoudre l'équation suivante:
a sin(x) + b = cot(x)
Merci d'avance pour votre aide!
mathelot a écrit:evidemment, il y a une infinité de solutions car
cotangente prend les valeurs de -infini à +infini périodiquement, tandis
que a sin(x)+b reste bornée
Je reformule ma question:
Pour a et b réels donnés et x réel strictement compris entre 0 et PI, calculer x en fonction de a et b sachant que :
a sin(x) + b = cot(x)
Je pense qu'il y aura maximum 2 solutions.
Je voix comment développer pour arriver aux équations que vous me donner, mais c'est après que je suis bloqué, comment arriver de là à obtenir x en fonction de a et b?
Merci!
jal3ous a écrit::
Pour a et b réels donnés et x réel strictement compris entre 0 et PI, calculer x en fonction de a et b sachant que :
a sin(x) + b = cot(x)
Je pense qu'il y aura maximum 2 solutions.
mais , non. je viens de t'expliquer pourquoi.
a sin(x)+ b est bornée (majorée par |a|+|b|)
et cotangente oscille entre -infini et +infini
euh, ton cot(x) ne serait pas un cosinus ??
mathelot a écrit:mais , non. je viens de t'expliquer pourquoi.
a sin(x)+ b est bornée (majorée par |a|+|b|)
et cotangente oscille entre -infini et +infini
euh, ton cot(x) ne serait pas un cosinus ??
Non c'est bien une cotangente.
Si on prend en exemple l'équation: sin (x) = x + 1 - PI/2
sin (x) est bornée, x + 1 - PI/2 ne l'est pas, et pourtant l équation a une seule solution: x = PI/2
Avec la méthode t=tan(x/2), je tombe moi aussi sur une équation du 4ème degré de paramètres a et b. Donc si on veut poursuivre, il faut utiliser la méthode de résolution du 4ème degré, bonne chance...
Mais si b = -a, il y a une solution évidente : t = 1. Donc x = Pi/2. Voilà une solution très particulière, c'est la seule que je puisse trouver...
Ah, une autre : si b = a, t = -1 est une solution évidente, donc x = -Pi/2.
jal3ous : s'agit-il d'un exercice, auquel cas on sait qu'il existe une façon de le résoudre, ou s'agit-il d'un calcul dont tu n'as pas la certitude qu'il y ait une résolution faisable ?
Mais si b = -a, il y a une solution évidente : t = 1. Donc x = Pi/2. Voilà une solution très particulière, c'est la seule que je puisse trouver...
Ah, une autre : si b = a, t = -1 est une solution évidente, donc x = -Pi/2.
jal3ous : s'agit-il d'un exercice, auquel cas on sait qu'il existe une façon de le résoudre, ou s'agit-il d'un calcul dont tu n'as pas la certitude qu'il y ait une résolution faisable ?
Robic a écrit:Avec la méthode t=tan(x/2), je tombe moi aussi sur une équation du 4ème degré de paramètres a et b. Donc si on veut poursuivre, il faut utiliser la méthode de résolution du 4ème degré, bonne chance...
Mais si b = -a, il y a une solution évidente : t = 1. Donc x = Pi/2. Voilà une solution très particulière, c'est la seule que je puisse trouver...
Ah, une autre : si b = a, t = -1 est une solution évidente, donc x = -Pi/2.
jal3ous : s'agit-il d'un exercice, auquel cas on sait qu'il existe une façon de le résoudre, ou s'agit-il d'un calcul dont tu n'as pas la certitude qu'il y ait une résolution faisable ?
Merci robic,
il s'agit d'un problème de physique que je cherche à résoudre et qui emmène après un peu de travail à cette forme d'équation mathématique; voici l'énoncée :
un projectile est lancé avec une vitesse initiale V et un angle (alpha) par rapport à un terrain plat (mais pas forcement horizontal). La portée du projectile sur ce terrain est L. calculer l'angle d'inclinaison (theta) du terrain par rapport à l'horizontal dans le plan de la trajectoire en fonction de V, alpha, L, et l'acceleration de la gravité g
c'est un problème dont je n'ai pas la certitude mais le fort sentiment qu'il y ait une résolution faisable...
Oui, en lisant cet énoncé je me dis que ça doit être faisable.
Est-ce que tu as l'équation de la trajectoire ? (C'est une parabole, donc c'est du second degré.) En gros il faudrait déterminer l'équation de cette parabole avec une droite passant par l'origine, et écrire la pente de cette droite en fonction de la distance de d'intersection à l'origine (L).
(Zut... Je viens de commencer un calcul, en calculant la distance entre l'origine et un point quelconque de cette trajectoire (destiné à jouer le rôle du point de chute) à un instant t, donc en calculant L=x²+z², et j'ai du t^4 qui apparaît. Aïe... Hé, mais je n'ai pas de termes de degré 1 et 0, donc ça devrait être bon en factorisant... ah si, il y a le L qui joue le rôle d'un terme de degré 0, crotte de bique... Pas moyen d'y échapper.)
Est-ce que tu as l'équation de la trajectoire ? (C'est une parabole, donc c'est du second degré.) En gros il faudrait déterminer l'équation de cette parabole avec une droite passant par l'origine, et écrire la pente de cette droite en fonction de la distance de d'intersection à l'origine (L).
(Zut... Je viens de commencer un calcul, en calculant la distance entre l'origine et un point quelconque de cette trajectoire (destiné à jouer le rôle du point de chute) à un instant t, donc en calculant L=x²+z², et j'ai du t^4 qui apparaît. Aïe... Hé, mais je n'ai pas de termes de degré 1 et 0, donc ça devrait être bon en factorisant... ah si, il y a le L qui joue le rôle d'un terme de degré 0, crotte de bique... Pas moyen d'y échapper.)
Robic a écrit:Oui, en lisant cet énoncé je me dis que ça doit être faisable.
Est-ce que tu as l'équation de la trajectoire ? (C'est une parabole, donc c'est du second degré.) En gros il faudrait déterminer l'équation de cette parabole avec une droite passant par l'origine, et écrire la pente de cette droite en fonction de la distance de d'intersection à l'origine (L).
(Zut... Je viens de commencer un calcul, en calculant la distance entre l'origine et un point quelconque de cette trajectoire (destiné à jouer le rôle du point de chute) à un instant t, donc en calculant L=x²+z², et j'ai du t^4 qui apparaît. Aïe... Hé, mais je n'ai pas de termes de degré 1 et 0, donc ça devrait être bon en factorisant... ah si, il y a le L qui joue le rôle d'un terme de degré 0, crotte de bique... Pas moyen d'y échapper.)
Eh oui, je tombe moi aussi sur du 4eme degré complet sauf le terme de degré 1, quasi impossible à resoudre symboliquement. en essayant d'autres maneuvres et différents repères pour arriver à une forme plus simple, je tombe sur l'equation trigonometrique du haut; plus compacte certes mais peut être pas plus simple finalement... :mur:
Ce qui me tarraude le plus c'est que la formule donnant la portée du projectile sur un plan incliné est bien connue mais je n'arrive pas à trouver sur internet une methode pour déduire l'inclinaison à partir de la portée...
Au fait : ce qu'on appelle la portée, c'est la distance spatiale entre le point de départ et le point d'arrivée (au sol) du projectile, ou bien c'est juste la distance en x ? Dans le deuxième cas, ça semble beaucoup plus simple.
Tiens, je le fais dans le deuxième cas. Donc je me place dans un repère Oxz et je suppose que l'origine est placée au point de départ. Dans ce cas, la parabole a pour équation (si je ne m'abuse) :
x)
Donc pour :
pour :
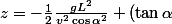L) .
.
L'angle de la pente est tel que :
de la pente est tel que :
L}{L} = -\frac{1}{2}\frac{gL}{v^2\cos\alpha^2}+\tan \alpha)
Je ne serais pas étonné que ce soit plutôt ça...
Tiens, je le fais dans le deuxième cas. Donc je me place dans un repère Oxz et je suppose que l'origine est placée au point de départ. Dans ce cas, la parabole a pour équation (si je ne m'abuse) :
Donc
L'angle
Je ne serais pas étonné que ce soit plutôt ça...
Robic a écrit:Au fait : ce qu'on appelle la portée, c'est la distance spatiale entre le point de départ et le point d'arrivée (au sol) du projectile, ou bien c'est juste la distance en x ? Dans le deuxième cas, ça semble beaucoup plus simple.
Tiens, je le fais dans le deuxième cas. Donc je me place dans un repère Oxz et je suppose que l'origine est placée au point de départ. Dans ce cas, la parabole a pour équation (si je ne m'abuse) :
Doncpour :
.
L'anglede la pente est tel que :
Je ne serais pas étonné que ce soit plutôt ça...
effectivement c'est bien plus simple dans ce cas mais la portée est la distance spatiale...
Wikipédia est de mon côté : http://fr.wikipedia.org/wiki/Port%C3%A9e_%28balistique%29 : « La portée est donc la projection horizontale d'une trajectoire courbe en trois dimensions. »
Robic a écrit:Wikipédia est de mon côté : http://fr.wikipedia.org/wiki/Port%C3%A9e_%28balistique%29 : « La portée est donc la projection horizontale d'une trajectoire courbe en trois dimensions. »
oui mais dans ma question (ça ne s'appelle peut être pas "portée" alors), je parle bien de la distance spatiale entre le point de départ et le point d'arrivée, qu'on voit dans le paragraphe 2.2 de cet article:
http://en.wikipedia.org/wiki/Trajectory#Uphill.2Fdownhill_in_uniform_gravity_in_a_vacuum
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

