Equation a^x = x^a
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 15 Oct 2005, 12:57
par Anonyme » 15 Oct 2005, 12:57
Hello, j'aurai besoin d'aide sur la résolution d'une équation:
a étant une constante, on cherche l'ensemble des x vérifiant:
a^x = x^a
je n'arrive à rien d'intéressant.. toute aide sera la bienvenue
merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Oct 2005, 13:01
par Nightmare » 15 Oct 2005, 13:01
Bonjour :happy3:
Les solutions ne sont pas triviales.
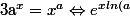}=e^{aln(x)}\Leftrightarrow xln(a)=aln(x)\Leftrightarrow \frac{ln(x)}{x}=\frac{a}{ln(a)})
Maintenant reste à connaître une réciproque de x->ln(x)/x ce qui n'est pas une mince affaire ...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Oct 2005, 13:07
par Nightmare » 15 Oct 2005, 13:07
Avec la fonction Oméga de Lambert :
}{x}=\frac{a}{ln(a)}\Leftrightarrow \frac{x}{\exp(x)}=\exp\(\frac{a}{ln(a)}\)\Leftrigh-x.\exp(-x)=-\exp\(\frac{a}{ln(a)}\)\Leftrightarrow x=-\Omega\(-\exp\(\frac{a}{ln(a)}\)\))
-
Anonyme
 par Anonyme » 15 Oct 2005, 13:24
par Anonyme » 15 Oct 2005, 13:24
xln(a)=aln(x) <=> ln(x)/x=a/ln(a) ??? tu as du te tromper, cela fait plutôt
<=>
ln(x)/x=ln(a)/a , ce qui change la donne..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Oct 2005, 13:39
par Nightmare » 15 Oct 2005, 13:39
Oui une étourderie de ma part, mais ça ne change pas grand chose, l'utilisation de la fonction non-usuelle Oméga s'impose
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Oct 2005, 13:43
par Nightmare » 15 Oct 2005, 13:43
Non en fait pas besoin d'Oméga.
On peut montrer que x->ln(x)/x est injective
ainsi :
ln(x)/x=ln(a)/a => x=a
Unique solution : x=a
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 15 Oct 2005, 13:45
par Nightmare » 15 Oct 2005, 13:45
On aurait pu s'en sortir si x->ln(x)/x était injective mais ce n'est pas le cas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
