Equation somme de cosinus sinus

[Gr33n_Sn0w]

Bonjour a tous,

J'ai une equation d'exercice de première année d'IUT a laquelle je n'arrive pas a réponde.

Résoudre l'equation suivante

cos(x) + sqrt(3)*sin(x) = sqrt(2)

j'ai commencé par remplacer cos(x) par sin(x + Pi/2)

afin de pouvoir utiliser sin(p) + sin(q) mais je ne sais pas quoi faire du sqrt(3)

il faut arriver a 2sin(x + pi/6) mais je n'y arrive pas.

merci de votre aide et bonne journée

[Monsieur23]

Aloha

Tu peux réécrire ton équation


Ensuite, tu connais un y tel que sin(y) = 1/2 et cos(y) = sqrt(3)/2

[Gr33n_Sn0w]

donc je suis arrivé a :

sin(pi\6) * cos(x) + sin(x) * cos(pi/6) = sqrt(2)/2

puis j'arrive a :

sin(x + pi/6) + sin(x - pi/6) = sqrt(2)/2

mais ici j'ai du faire une erreur car j'arrive au final avec

2sin(x + pi/6) * cos( pi/12 ) = sqrt(2)/2

il y a se cos ( pi/12 ) "en trop"

[BiancoAngelo]

donc je suis arrivé a :

sin(pi\6) * cos(x) + sin(x) * cos(pi/6) = sqrt(2)/2

puis j'arrive a :

sin(x + pi/6) + sin(x - pi/6) = sqrt(2)/2

mais ici j'ai du faire une erreur car j'arrive au final avec

2sin(x + pi/6) * cos( pi/12 ) = sqrt(2)/2

il y a se cos ( pi/12 ) "en trop"

Quand tu as sin(pi\6) * cos(x) + sin(x) * cos(pi/6) = sqrt(2)/2, tu peux peut-être utiliser une formule du genre sin(a+b) = ...
Qu'en penses-tu ?

[Joker62]

Hello,

Une autre façon qui revient au même :

Remarquer que :

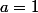
Ici et d'où

D'où

[Gr33n_Sn0w]

En effet je cherche toujours trop compliqué

mon equation est de la forme sin(a)*cos(b)+sin(b)*cos(a)

est donc sin(x + pi/6 ) = sqrt(2)/2

et donc les solutions sont x1= pi/12 et x2 = 7*pi/12

merci beaucoup pour votre aide !

[chan79]

En effet je cherche toujours trop compliqué

mon equation est de la forme sin(a)*cos(b)+sin(b)*cos(a)

est donc sin(x + pi/6 ) = sqrt(2)/2

et donc les solutions sont x1= pi/12 et x2 = 7*pi/12

merci beaucoup pour votre aide !

oui, mais n'oublie pas les ...

[Gr33n_Sn0w]

oui, mais n'oublie pas les ...

c'est vrai j'oublie tout le temps merci