Equation de reccurence

[adeniss]

Bonjour,
j'aurais besoin d'un coup de main pour resoudre les equations de reccurence:
u(n+1)=u(n)+2n+3 avec u0=1,n>=0
u(n+1)=u(n)+3n²-n avec u0=3,n>=0
u(n+1)=2u(n)+5 avec u0=1,n>=0
u(n+1)=2u(n)+2^n,u0=1,n>=0

[zygomatique]

salut

u(1) = u(0) + 2 * 0 + 3
u(2) = u(1) + 2 * 1 + 3
u(3) = u(2) + 2 * 2 + 3
....
u(n - 1) = u(n - 2) + 2(n - 2) + 3
u(n) = u(n - 1) + 2(n - 1) + 3
-------------------------------------


il suffit d'additionner membre à membre .... et simplifier ....


idem pour le deuxième


pour le troisième

tu poses u(n) = v(n) + a où a est un réel et tu détermines a tel que la suite (v_n) soit géométrique

[mathelot]

pour la (4)






...



on multiplie la seconde égalité par 2, la troisième par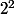 , la dernière par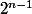
on trouve

hint:
u_n=2^n+n 2^{n-1}

[adeniss]

salut

u(1) = u(0) + 2 * 0 + 3
u(2) = u(1) + 2 * 1 + 3
u(3) = u(2) + 2 * 2 + 3
....
u(n - 1) = u(n - 2) + 2(n - 2) + 3
u(n) = u(n - 1) + 2(n - 1) + 3
-------------------------------------


il suffit d'additionner membre à membre .... et simplifier ....


idem pour le deuxième


pour le troisième

tu poses u(n) = v(n) + a où a est un réel et tu détermines a tel que la suite (v_n) soit géométrique

Je dois additioner u(n)+u(n-1)+....+u(0). ?
concernant a on le donne nous meme ou on le laisse tel quel?

[mathelot]

Je dois additioner u(n)+u(n-1)+....+u(0). ?
concernant a on le donne nous meme ou on le laisse tel quel?

tu fais "comme si" tu additionnais les égalités, mais immédiatement après
tu simplifies tous les termes sauf deux.

on choisit "a" solution d'une équation à déterminer.

[adeniss]

Je trouve pas comment faire.

[mathelot]

Je trouve pas comment faire.

on va prendre un autre exemple plus simple

on écrit les n égalités



....
....


on compte n égalités. On les additionne membres à membres:


on simplifie